Нормально распределенный и некоррелированный не означает независимого - Normally distributed and uncorrelated does not imply independent

В теория вероятности, хотя простые примеры показывают, что линейная некоррелированность двух случайных величин, как правило, не подразумевает их независимость, иногда ошибочно думают, что это означает, что когда две случайные величины нормально распределенный. В этой статье показано, что предположение о нормальном распределении не имеет таких последствий, хотя многомерное нормальное распределение, в том числе двумерное нормальное распределение, делает.

Сказать, что пара ${\displaystyle (X,Y)}$ случайных величин имеет двумерное нормальное распределение означает, что каждый линейная комбинация ${\displaystyle aX+bY}$ из ${\displaystyle X}$ и ${\displaystyle Y}$ для постоянных (т.е. не случайных) коэффициентов ${\displaystyle a}$ и ${\displaystyle b}$ имеет одномерное нормальное распределение. В том случае, если ${\displaystyle X}$ и ${\displaystyle Y}$ некоррелированы, то они независимы.^[1] Однако возможно для двух случайных величин ${\displaystyle X}$ и ${\displaystyle Y}$ должны быть распределены таким образом совместно, чтобы каждый из них по отдельности имел нормальное распределение, и они не коррелировали, но не были независимыми; примеры приведены ниже.

Примеры

Симметричный пример

Совместный ассортимент ${\displaystyle X}$ и ${\displaystyle Y}$. Более темный цвет означает более высокое значение функции плотности.

Предполагать ${\displaystyle X}$ имеет нормальное распределение с ожидаемое значение 0 и дисперсия 1. Пусть ${\displaystyle W}$ иметь Распределение Радемахера, так что ${\displaystyle W=1}$ или же ${\displaystyle W=-1}$, каждое с вероятностью 1/2, и положим ${\displaystyle W}$ не зависит от ${\displaystyle X}$. Позволять ${\displaystyle Y=WX}$. потом

• ${\displaystyle X}$ и ${\displaystyle Y}$ некоррелированы;
• оба имеют одинаковое нормальное распределение; и
• ${\displaystyle X}$ и ${\displaystyle Y}$ не являются независимыми.^[2]

Чтобы увидеть это ${\displaystyle X}$ и ${\displaystyle Y}$ некоррелированы, можно считать ковариация ${\displaystyle \operatorname {cov} (X,Y)}$: по определению, это

${\displaystyle \operatorname {cov} (X,Y)=\operatorname {E} (XY)-\operatorname {E} (X)\operatorname {E} (Y).}$

Тогда по определению случайных величин ${\displaystyle X}$, ${\displaystyle Y}$, и ${\displaystyle W}$, и независимость ${\displaystyle W}$ из ${\displaystyle X}$, надо

${\displaystyle \operatorname {cov} (X,Y)=\operatorname {E} (XY)-0=\operatorname {E} (X^{2}W)=\operatorname {E} (X^{2})\operatorname {E} (W)=\operatorname {E} (X^{2})\cdot 0=0.}$

Чтобы увидеть это ${\displaystyle Y}$ имеет то же нормальное распределение, что и ${\displaystyle X}$, учитывать

${\displaystyle {\begin{aligned}\Pr(Y\leq x)&{}=\operatorname {E} (\Pr(Y\leq x\mid W))\\&{}=\Pr(X\leq x)\Pr(W=1)+\Pr(-X\leq x)\Pr(W=-1)\\&{}=\Phi (x)\cdot {\frac {1}{2}}+\Phi (x)\cdot {\frac {1}{2}}\end{aligned}}}$

(поскольку ${\displaystyle X}$ и ${\displaystyle -X}$ оба имеют одинаковое нормальное распределение), где ${\displaystyle \Phi (x)}$ это кумулятивная функция распределения нормального распределения ..

Чтобы увидеть это ${\displaystyle X}$ и ${\displaystyle Y}$ не являются независимыми, обратите внимание, что ${\displaystyle |Y|=|X|}$ или это ${\displaystyle \operatorname {Pr} (Y>1|X=1/2)=\operatorname {Pr} (X>1|X=1/2)=0}$.

Наконец, распределение простой линейной комбинации ${\displaystyle X+Y}$ концентрирует положительную вероятность в 0: ${\displaystyle \operatorname {Pr} (X+Y=0)=1/2}$. Следовательно, случайная величина ${\displaystyle X+Y}$ не распространяется нормально, и поэтому ${\displaystyle X}$ и ${\displaystyle Y}$ не совместно нормально распределены (по определению выше).

Асимметричный пример

Совместная плотность ${\displaystyle X}$ и ${\displaystyle Y}$. Темнее означает более высокое значение плотности.

Предполагать ${\displaystyle X}$ имеет нормальное распределение с ожидаемое значение 0 и дисперсия 1. Пусть

${\displaystyle Y=\left\{{\begin{matrix}X&{\text{if }}\left|X\right|\leq c\\-X&{\text{if }}\left|X\right|>c\end{matrix}}\right.}$

куда ${\displaystyle c}$ - положительное число, которое необходимо указать ниже. Если ${\displaystyle c}$ очень маленький, то корреляция ${\displaystyle \operatorname {corr} (X,Y)}$ рядом ${\displaystyle -1}$ если ${\displaystyle c}$ очень большой, то ${\displaystyle \operatorname {corr} (X,Y)}$ близко к 1. Поскольку корреляция непрерывная функция из ${\displaystyle c}$, то теорема о промежуточном значении подразумевает, что есть определенная ценность ${\displaystyle c}$ что делает корреляцию 0. Это значение составляет приблизительно 1,54. В таком случае, ${\displaystyle X}$ и ${\displaystyle Y}$ некоррелированы, но они явно не независимы, поскольку ${\displaystyle X}$ полностью определяет ${\displaystyle Y}$.

Чтобы увидеть это ${\displaystyle Y}$ нормально распределен - действительно, его распределение такое же, как у ${\displaystyle X}$ - каждый может вычислить его кумулятивная функция распределения:

${\displaystyle {\begin{aligned}\Pr(Y\leq x)&=\Pr(\{|X|\leq c{\text{ and }}X\leq x\}{\text{ or }}\{|X|>c{\text{ and }}-X\leq x\})\\&=\Pr(|X|\leq c{\text{ and }}X\leq x)+\Pr(|X|>c{\text{ and }}-X\leq x)\\&=\Pr(|X|\leq c{\text{ and }}X\leq x)+\Pr(|X|>c{\text{ and }}X\leq x)\\&=\Pr(X\leq x),\end{aligned}}}$

где предпоследнее равенство следует из симметрии распределения ${\displaystyle X}$ и симметрия условия, что ${\displaystyle |X|\leq c}$.

В этом примере разница ${\displaystyle X-Y}$ далеки от нормального распределения, поскольку имеет значительную вероятность (около 0,88) того, что оно равно 0. Напротив, нормальное распределение, будучи непрерывным распределением, не имеет дискретной части, то есть не концентрируется более чем нулевая вероятность в любой точке. как следствие ${\displaystyle X}$ и ${\displaystyle Y}$ не совместно нормально распространяются, даже если они нормально распространяются отдельно.^[3]

Примеры с поддержкой почти везде в ℝ²

Как известно, соотношение ${\displaystyle C}$ двух независимых стандартных нормальных случайных отклонений ${\displaystyle X_{i}}$ и ${\displaystyle Y_{i}}$ имеет Распределение Коши. С равным успехом можно начать со случайной величины Коши ${\displaystyle C}$ и вывести условное распределение ${\displaystyle Y_{i}}$ чтобы удовлетворить требование, чтобы ${\displaystyle X_{i}=CY_{i}}$ с ${\displaystyle X_{i}}$ и ${\displaystyle Y_{i}}$ независимые и стандартные нормальные. Проворачивая математику, можно обнаружить, что

${\displaystyle Y_{i}=W_{i}{\sqrt {\frac {\chi _{i}^{2}\left(k=2\right)}{1+C^{2}}}}}$

в котором ${\displaystyle W_{i}}$ является случайной величиной Радемахера и ${\displaystyle \chi _{i}^{2}\left(k=2\right)}$ это Случайная величина хи-квадрат с двумя степенями свободы.

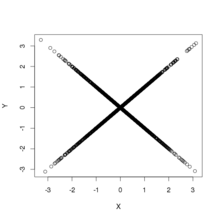
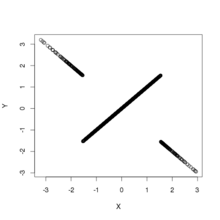
Рассмотрим два набора ${\displaystyle \left(X_{i},Y_{i}\right)}$, ${\displaystyle i\in \left\{1,2\right\}}$. Обратите внимание, что ${\displaystyle C}$ не индексируется ${\displaystyle i}$ - то есть та же случайная величина Коши ${\displaystyle C}$ используется в определении обоих ${\displaystyle \left(X_{1},Y_{1}\right)}$ и ${\displaystyle \left(X_{2},Y_{2}\right)}$. Это разделение ${\displaystyle C}$ приводит к зависимостям по индексам: ни ${\displaystyle X_{1}}$ ни ${\displaystyle Y_{1}}$ не зависит от ${\displaystyle Y_{2}}$. Тем не менее все ${\displaystyle X_{i}}$ и ${\displaystyle Y_{i}}$ некоррелированы, поскольку все двумерные распределения обладают симметрией отражения по осям.

Ненормальные совместные распределения с нормальными краями.

На рисунке показаны диаграммы рассеяния выборок, взятых из вышеуказанного распределения. Это дает два примера двумерных распределений, которые некоррелированы и имеют нормальные предельные распределения, но не являются независимыми. На левой панели показано совместное распределение ${\displaystyle X_{1}}$ и ${\displaystyle Y_{2}}$; дистрибутив поддерживается везде, но не у истоков. На правой панели показано совместное распределение ${\displaystyle Y_{1}}$ и ${\displaystyle Y_{2}}$; распределение имеет поддержку везде, кроме осей, и имеет разрыв в начале координат: плотность расходится при приближении к началу координат по любому прямому пути, кроме осей.

Смотрите также

• Корреляция и зависимость

Рекомендации

1. Хогг, Роберт; Танис, Эллиот (2001). «Глава 5.4. Двумерное нормальное распределение». Вероятность и статистический вывод (6-е изд.). С. 258–259. ISBN  0130272949.
2. UIUC, Лекция 21. Многомерное нормальное распределение, 21.6: «Индивидуально гауссовский против совместно гауссовского».
3. Эдвард Л. Мельник и Аарон Тененбейн, «Неправильные спецификации нормального распределения», Американский статистик, том 36, номер 4 ноября 1982 года, страницы 372–373