Метод максимального давления пузырька - Maximum bubble pressure method

В физика, то метод максимального давления пузырька, или короче метод пузырькового давления, это метод измерения поверхностное натяжение из жидкость, с поверхностно-активные вещества.

Фон

Когда жидкость образует интерфейс с газ фаза, а молекула на границе есть совсем другие физические свойства из-за разбаланса сил притяжения соседними молекулами. На состояние равновесия жидкости внутренние молекулы находятся под уравновешенными силами с равномерно распределенными соседними молекулами.

Однако относительно меньшее количество молекул в газовой фазе над границей раздела, чем конденсированный жидкая фаза составляет общую сумму силы наносится на поверхностную молекулу непосредственно внутри жидкости, и, таким образом, поверхностные молекулы стремятся минимизировать свою площадь поверхности.

Такое неравенство молекулярных сил вызывает непрерывное движение молекул изнутри к поверхности, что означает, что молекулы поверхности имеют дополнительные энергия, который называется поверхностная свободная энергия или же потенциальная энергия,^{[который? ]} и такая энергия, действующая на уменьшенную единицу площади, определяется как поверхностное натяжение.

Это основа для интерпретации соответствующих явлений, возникающих на поверхности или на границе раздела материалов, и множество методов для измерения поверхностное натяжение была разработана.^[1]

Среди различных способов определения поверхностного натяжения, Метод кольца Дю Нюи и Метод слайдов Вильгельми основаны на разделении твердый объект с поверхности жидкости, и Подвесной метод падения и Sessile drop или пузырьковый метод зависит от деформация сферической формы капли жидкости.^[1]

Несмотря на то, что эти методы относительно просты и обычно используются для определения статический поверхностное натяжение, в случае добавления примесей в жидкость измерение поверхностного натяжения на основе динамическое равновесие следует наносить, так как для получения полностью сформированной поверхности требуется больше времени, а это означает, что трудно достичь статического равновесия, как это делает чистая жидкость.^[2]

Наиболее типичная примесь, вызывающая динамичный поверхностное натяжение измерение представляет собой молекулу поверхностно-активного вещества, которая имеет оба из гидрофильный сегмент, обычно называемый «головной группой» и гидрофобный сегмент, обычно называемый «хвостовой группой» в той же молекуле. Из-за характеристики молекулярная структура, поверхностно-активные вещества мигрируют к поверхности жидкости, граничащей с газовой фазой, до тех пор, пока внешняя сила не рассеивает накопленные молекулы от границы раздела или поверхность не будет полностью занята и, таким образом, не сможет вместить дополнительные молекулы. Во время этого процесса поверхностное натяжение уменьшается со временем и, наконец, приближается к равновесному поверхностному натяжению (σ_{равновесие}).^[3] Такой процесс показан на рисунке 1. (Изображение было воспроизведено по ссылке)^[2]

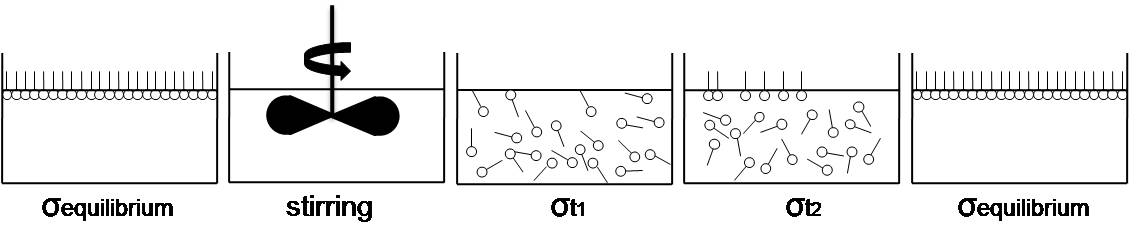
Рисунок 1 - Миграция молекул ПАВ и изменение поверхностного натяжения (σ_t1 > σ_t2 > σ_{равновесие})

Метод максимального давления пузырька

Одним из полезных методов определения динамического поверхностного натяжения является измерение «метода максимального давления пузырька» или, проще говоря, метода давления пузырька.^[1][2]

Давление пузыря тензиометр создает пузырьки газа (например, воздуха) с постоянной скоростью и продувает их через капилляр, который погружен в жидкость пробы, и его радиус уже известен.

В давление (п) внутри газового пузыря продолжает увеличиваться, и максимальное значение достигается, когда пузырек имеет полностью полусферическую форму, радиус которой точно соответствует радиусу капилляра.^[3]

На рисунке 2 показан каждый этап образования пузырька и соответствующее изменение радиуса пузырька, и каждый этап описан ниже. (Изображение было воспроизведено по ссылке)^[2][3]

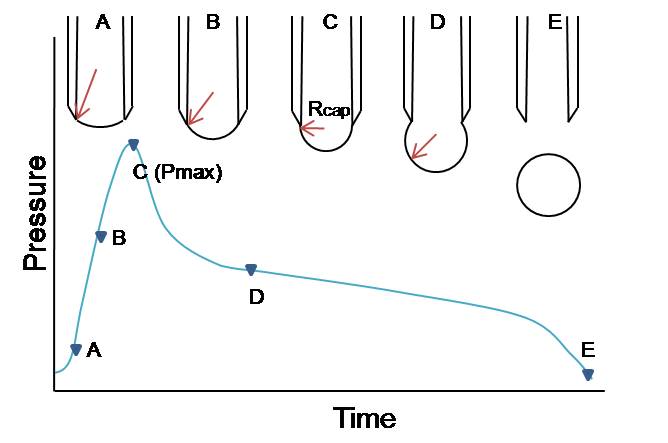
Рисунок 2 - Изменение давления во время образования пузырьков в зависимости от времени.

A, B: на конце капилляра появляется пузырек. По мере увеличения размера радиус кривизны пузыря уменьшается.

C: В точке максимального давления пузырька пузырь имеет полную полусферическую форму, радиус которой идентичен радиусу капилляра, обозначенному Rcap. Поверхностное натяжение можно определить с помощью Уравнение Юнга – Лапласа в уменьшенная форма для сферической формы пузырьков в жидкости.^[3]

${\displaystyle \sigma ={\frac {\Delta P_{\rm {max}}\times R_{\rm {cap}}}{2}}}$

(σ: поверхностное натяжение, Δп_{Максимум}: максимальное падение давления, р_{колпачок}: радиус капилляра)

D, E: после достижения максимального давления давление пузыря уменьшается, а радиус пузыря увеличивается до тех пор, пока пузырек не отделится от конца капилляра и не начнется новый цикл. Это не имеет отношения к определению поверхностного натяжения.^[3]

Тензиометры, разработанные в настоящее время и выпускаемые на рынок, контролируют давление, необходимое для образования пузырька, разность давлений внутри и снаружи пузырька, радиус пузырька и поверхностное натяжение образца рассчитываются за один раз, а сбор данных осуществляется через ПК контроль.

Метод пузырькового давления обычно используется для измерения динамического поверхностного натяжения системы, содержащей поверхностно-активные вещества или другие примеси, поскольку он не требует измерения угла смачивания и имеет высокую точность, даже если измерение выполняется быстро.^[1][3] «Метод пузырькового давления» может применяться для измерения динамического поверхностного натяжения, особенно для систем, содержащих поверхностно-активные вещества.^[3] Более того, этот метод подходит для биологические жидкости подобно сыворотка^{[который? ]} потому что для измерений не требуется большого количества жидкой пробы.^[4] Наконец, этот метод используется для косвенного определения содержания поверхностно-активного вещества в промышленных ваннах для очистки или нанесения покрытий, поскольку динамическое поверхностное натяжение в конкретном диапазоне скоростей образования пузырьков показывает сильную корреляцию с концентрацией. ^[2]

Рекомендации

1. Адамсон, Артур В .; Алиса П. Гаст (1997). Физическая химия поверхностей (6-е изд.). Wiley Interscience.
2. Метод пузырькового давления на kruss-scientific.com
3. Динамические методы на lauda.de
4. Хаббард, Артур Т. (2002). Энциклопедия науки о поверхности и коллоидах (Том 1). CRC Press, стр. 814–815

внешняя ссылка

• Принцип измерения и области применения измерения динамического поверхностного натяжения тензиометром давления пузырьков
• Метод пузырькового давления для измерения динамического поверхностного натяжения