Формула прироста масонов - Masons gain formula
Формула усиления Мейсона (MGF) это метод поиска функция передачи линейного график потока сигналов (SFG). Формула была получена Сэмюэл Джефферсон Мейсон,[1] в честь кого он также назван. MGF - это альтернативный метод алгебраического нахождения передаточной функции путем маркировки каждого сигнала, записи уравнения того, как этот сигнал зависит от других сигналов, а затем решения нескольких уравнений для выходного сигнала в терминах входного сигнала. MGF предоставляет пошаговый метод получения передаточной функции из SFG. Часто MGF можно определить путем проверки SFG. Этот метод может легко обрабатывать SFG с множеством переменных и циклов, включая циклы с внутренними циклами. MGF часто возникает в контексте Системы управления и цифровые фильтры, поскольку системы управления и цифровые фильтры часто представлены SFG.
Формула
Формула усиления выглядит следующим образом:
куда:
- Δ = определитель графа.
- ув = переменная входного узла
- уиз = переменная выходного узла
- грамм = полное усиление между ув и уиз
- N = общее количество прямых путей между ув и уиз
- граммk = усиление пути kй прямой путь между ув и уиз
- Lя = усиление каждого замкнутого контура в системе
- LяLj = произведение коэффициентов усиления контура любых двух не касающихся контуров (без общих узлов)
- LяLjLk = произведение коэффициентов усиления любых трех попарно не соприкасающихся петель
- Δk = значение кофактора Δ для kth прямой путь, при этом петли касаются kth прямой путь удален. *
Определения[2]
- Путь: непрерывный набор ветвей, пересекаемых в указанном ими направлении.
- Прямой путь: путь от входного узла к выходному узлу, в котором ни один из узлов не затрагивается более одного раза.
- Цикл: путь, который начинается и заканчивается на одном узле, в котором ни один узел не затрагивается более одного раза.
- Прирост на пути: результат прироста всех ветвей на пути.
- Коэффициент усиления петли: произведение коэффициентов усиления всех ветвей петли.
Процедура поиска решения
- Составьте список всех путей продвижения и их достижений и пометьте их. граммk.
- Составьте список всех петель и их усиления и пометьте их Lя (за я петли). Составьте список всех пар не касающихся петель и произведений их выигрышей (LяLj). Составьте список всех попарно не соприкасающихся петель, взятых по три за раз (LяLjLk), затем по четыре и так далее, пока их больше не будет.
- Вычислить определитель Δ и сомножители Δk.
- Примените формулу.
Примеры
Схема, содержащая два порта

Передаточная функция от Vв к V2 желательно.
Есть только один прямой путь:
- Vв к V1 к я2 к V2 с прибылью
Есть три петли:
- V1 к я1 к V1 с прибылью
- V2 к я2 к V2 с прибылью
- V1 к я2 к V2 к я1 к V1 с прибылью
- Примечание: L1 и L2 не касайтесь друг друга, тогда как L3 касается обеих других петель.
- примечание: прямой путь касается всех петель, поэтому все, что осталось, 1.
Цифровой биквадратный БИХ-фильтр
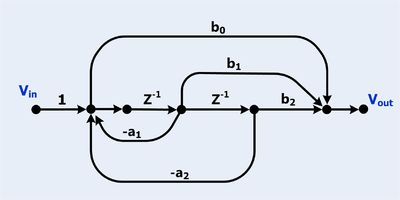
Цифровые фильтры часто изображаются в виде диаграмм потока сигналов.
- Есть две петли
- Обратите внимание, две петли соприкасаются, поэтому для их продукта нет термина.
- Есть три прямых пути
- Все прямые пути касаются всех петель, поэтому
Сервопривод

График потока сигналов имеет шесть петель. Они есть:
Есть один прямой путь:
Прямой путь касается всех петель, поэтому коэффициент
И усиление от входа к выходу равно
Эквивалентная матричная форма
Правило Мейсона можно сформулировать в простой матричной форме. Предполагать - переходная матрица графа, где это суммарный коэффициент пропускания ветвей от узла м к узлу п. Тогда выигрыш от узла м узел п графа равно , куда
- ,
и - единичная матрица.
Правило Мейсона также особенно полезно для получения передаточной функции в z-области дискретных сетей, которые имеют внутренние петли обратной связи, встроенные во внешние петли обратной связи (вложенные петли). Если дискретную сеть можно нарисовать в виде графа потока сигналов, то применение правила Мейсона даст передаточную функцию H (z) этой сети в z-области.
Сложность и вычислительные приложения
Правило Мейсона может увеличиваться факториально, потому что количество путей в ориентированном графе резко увеличивается. Чтобы убедиться в этом, рассмотрим полный ориентированный граф на вершины, имея ребро между каждой парой вершин. Есть форма пути к для каждого из перестановки промежуточных вершин. Таким образом Гауссово исключение в общем случае более эффективен.
Тем не менее, правило Мейсона характеризует передаточные функции взаимосвязанных систем одновременно алгебраическим и комбинаторным образом, что позволяет делать общие утверждения и другие вычисления в теории алгебраических систем. Хотя во время исключения по Гауссу происходит множество обратных событий, правило Мейсона естественным образом объединяет их в один квазиобратный. Общая форма
Где, как описано выше, представляет собой сумму продуктов цикла, каждый из которых обычно попадает в идеальный (например, строго причинные операторы). Фракции этой формы составляют подкольцо из поле рациональных функций. Это наблюдение переносится на некоммутативный случай,[3] хотя само правило Мэйсона должно быть заменено Правило Ригла.
Смотрите также
Примечания
- ^ Мейсон, Сэмюэл Дж. (Июль 1956 г.). «Теория обратной связи - дополнительные свойства графов потоков сигналов» (PDF). Труды IRE. 44 (7): 920–926. Дои:10.1109 / jrproc.1956.275147. HDL:1721.1/4778. S2CID 18184015.
- ^ Куо, Бенджамин С. (1967). Системы автоматического управления (2-е изд.). Прентис-Холл. С. 59–60.
- ^ Pliam, J.O. и Ли, Э.Б. (1995). «О глобальных свойствах взаимосвязанных систем». IEEE Trans. Circuits and Syst. я. 42 (12): 1013–1017. Дои:10.1109/81.481196.CS1 maint: использует параметр авторов (связь)
Рекомендации
- Болтон, В. Ньюнес (1998). Справочник по технике управления. Оксфорд: Newnes.
- Ван Валкенбург, М. Э. (1974). Сетевой анализ (3-е изд.). Энглвуд Клиффс, Нью-Джерси: Прентис-Холл.






























![t _ {{нм}} = left [{ mathbf {T}} right] _ {{нм}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafc8cf92f03a9ca2f0c2b992bc48f3920a57216)
![u _ {{нм}} = left [{ mathbf {U}} right] _ {{нм}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f97f4ff65eedb74a0f1d55973dc31a56d4ff01c)








