Langleys Adventitious Angles - Langleys Adventitious Angles

Дополнительные углы Лэнгли математическая проблема, поставленная Эдвард Манн Лэнгли в Математический вестник в 1922 г.[1][2]
Проблема
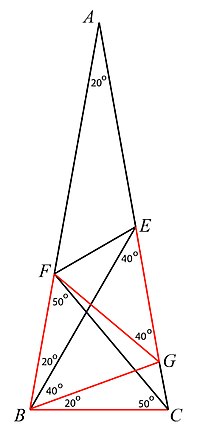
В исходном виде проблема была следующей:
- является равнобедренный треугольник.
- в к порезы в
- в к порезы в
Решение
Решение было разработано Джеймс Мерсер в 1923 г.[2] Это решение включает в себя рисование одной дополнительной линии и повторное использование того факта, что внутренние углы треугольника в сумме составляют 180 °, чтобы доказать, что все треугольники, нарисованные внутри большого треугольника, равнобедренные.
- Рисовать в к пересекающийся в и нарисовать (См. Рисунок внизу справа.)
- С и тогда и треугольник равнобедренный с
- С и тогда и треугольник равнобедренный с
- С и затем треугольник является равносторонний.
- С и тогда и треугольник равнобедренный с
- Следовательно, все красные линии на рисунке равны.
- С треугольник равнобедренный с
- Следовательно
Возможны многие другие решения. Разрежьте узел, перечислите двенадцать различных решений и несколько альтернативных задач с одним и тем же треугольником 80-80-20, но с разными внутренними углами.[4]
Обобщение
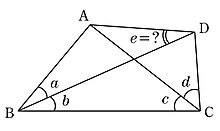
Четырехугольник, такой как BCEF, называется придаточный четырехугольник когда углы между диагоналями и сторонами равны рациональным углам, углам, которые дают рациональное число при измерении в градусах или других единицах, для которых весь круг является рациональным числом. Были построены многочисленные дополнительные четырехугольники, помимо того, что фигурирует в головоломке Лэнгли. Они образуют несколько бесконечных семейств и дополнительный набор единичных примеров.[5]
Классификация дополнительных четырехугольников (которые не обязательно должны быть выпуклыми) оказывается эквивалентной классификации всех тройных пересечений диагоналей в правильные многоугольники. Это было решено Геррит Бол в 1936 г. (Beantwoording van prijsvraag # 17, Nieuw-Archief voor Wiskunde 18, стр. 14-66). Фактически он классифицировал (хотя и с некоторыми ошибками) все множественные пересечения диагоналей правильными многоугольниками. Его результаты (все сделанные вручную) были подтверждены компьютером, а ошибки исправлены Бьорном Пуненом и Майклом Рубинштейном в 1998 году.[6] В статье представлена история проблемы и фото с обычным триаконтагон и его диагонали.
В 2015 году анонимная японка под псевдонимом «aerile re» опубликовала первый известный метод (метод трех центров окружности) для построения доказательства в элементарной геометрии для особого класса задач о придаточных четырехугольниках.[7][8][9] Эта работа решает первую из трех нерешенных проблем, перечисленных Ригби в его статье 1978 года.[5]
Рекомендации
- ^ а б Лэнгли, Э.М. (1922), «Проблема 644», Математический вестник, 11: 173.
- ^ а б c Дорогой, Дэвид (2004), Универсальная книга математики: от абракадабры до парадоксов Зенона, John Wiley & Sons, стр. 180.
- ^ Трипп, Колин (1975), «Дополнительные углы», Математический вестник, 59: 98–106, JSTOR 3616644.
- ^ Богомольный Александр. "Треугольник 80-80-20". www.cut-the-knot.org. Получено 2018-06-03.
- ^ а б Ригби, Дж. Ф. (1978), «Придаточные четырехугольники: геометрический подход», Математический вестник, 62 (421): 183–191, Дои:10.2307/3616687, МИСТЕР 0513855.
- ^ Пунен, Бьорн; Рубинштейн, Майкл (1998), «Количество точек пересечения диагоналями правильного многоугольника» (PDF), Журнал SIAM по дискретной математике, 11 (1): 135–156.
- ^ Сайто, Хироши (2016), «Придаточные четырехугольники полностью решены элементарным решением», Гендаисугаку (現代 数学) (на японском языке), 49 (590): 66–73, ISSN 2187-6495.
- ^ aerile_re (2015-10-27), Последний вызов от Geometry the Great (на японском языке), заархивировано из оригинал на 2016-04-16.
- ^ Сайто, Хироши (2016-12-11), Представляем "метод трех окружностей по центру" - Английский перевод статьи из Гендаисугаку (現代 数学).
внешняя ссылка
- Угловой угол, MathPages




































