Итерационные петли трафарета - Iterative Stencil Loops

Форма 7-точечного 3D фон Нейман стиль трафарета.

Итерационные петли трафарета (ISL) - это класс решений для обработки численных данных.^[1]какое обновление элементы массива по некоторому фиксированному шаблону, называемому трафаретом.^[2] Чаще всего они встречаются в компьютерное моделирование, например для вычислительная гидродинамика в контексте научных и инженерных приложений. Другие известные примеры включают решение уравнения в частных производных,^[1] то Якоби ядро, Метод Гаусса – Зейделя,^[2] обработка изображений^[1] и клеточные автоматы.^[3] Регулярная структура массивов отличает методы трафарета от других методов моделирования, таких как Метод конечных элементов. Наиболее конечно-разностные коды которые работают в обычных сетях, могут быть сформулированы как ISL.

Определение

ISL выполняют последовательность разверток (называемых временными шагами) по заданному массиву.^[2] Обычно это 2- или 3-мерная регулярная сетка.^[3] Элементы массивов часто называют ячейками. На каждом временном шаге обновляются все элементы массива.^[2] Используя соседние элементы массива в фиксированном шаблоне (трафарете), вычисляется новое значение каждой ячейки. В большинстве случаев граничные значения остаются неизменными, но в некоторых случаях (например, LBM коды ) их также необходимо отрегулировать во время вычислений. Поскольку шаблон для каждого элемента одинаков, шаблон доступа к данным повторяется.^[4]

Более формально мы можем определить ISL как 5-кратный ${displaystyle (I, S, S_ {0}, s, T)}$ со следующим значением:^[3]

${displaystyle I = prod _ {i = 1} ^ {k} [0, ldots, n_ {i}]}$ - индексный набор. Он определяет топологию массива.
${displaystyle S}$ - это (не обязательно конечный) набор состояний, одно из которых каждая ячейка может принять на любом заданном временном шаге.
${displaystyle S_ {0} двоеточие mathbb {Z} ^ {k} o S}$ определяет начальное состояние системы в момент времени 0.
${displaystyle sin prod _ {i = 1} ^ {l} mathbb {Z} ^ {k}}$ является самим трафаретом и описывает фактическую форму окрестности. Есть ${displaystyle l}$ элементы в трафарете.
${displaystyle Tcolon S ^ {l} o S}$ - это функция перехода, которая используется для определения нового состояния ячейки в зависимости от ее соседей.

поскольку я это k-мерный целочисленный интервал, массив всегда будет иметь топологию конечной регулярной сетки. Массив также называется пространством моделирования, и отдельные ячейки идентифицируются своим индексом. ${displaystyle cin I}$ . Трафарет представляет собой упорядоченный набор ${displaystyle l}$ относительные координаты. Теперь мы можем получить для каждой ячейки ${displaystyle c}$ набор индексов его соседей ${displaystyle I_ {c}}$

{displaystyle I_ {c} = {jmid существует xin s: j = c + x},}

Их состояния задаются отображением кортежа ${displaystyle I_ {c}}$ в соответствующий набор состояний ${displaystyle N_ {i} (c)}$ , где ${displaystyle N_ {i} двоеточие I o S ^ {l}}$ определяется следующим образом:

{displaystyle N_ {i} (c) = (s_ {1}, ldots, s_ {l}) {ext {with}} s_ {j} = S_ {i} (I_ {c} (j)),}

Это все, что нам нужно для определения состояния системы для следующих временных шагов. ${displaystyle S_ {i + 1} двоеточие mathbb {Z} ^ {k} o S}$ с участием ${displaystyle iin mathbb {N}}$ :

{displaystyle S_ {i + 1} (c) = {egin {case} T (N_ {i} (c)), & cin I S_ {i} (c), & cin mathbb {Z} ^ {k} setminus Iend {case}}}

Обратите внимание, что ${displaystyle S_ {i}}$ определяется на ${displaystyle mathbb {Z} ^ {k}}$ и не только на ${displaystyle I}$ так как граничные условия также должны быть установлены. Иногда элементы ${displaystyle I_ {c}}$ может быть определен векторным сложением по модулю размерности пространства моделирования для реализации тороидальных топологий:

{displaystyle I_ {c} = {jmid существует xin s: j = ((c + x) mod (n_ {1}, ldots, n_ {k}))}}

Это может быть полезно для реализации периодические граничные условия, что упрощает некоторые физические модели.

Пример: итерация Якоби в 2D

Зависимости данных выбранной ячейки в 2D-массиве.

Чтобы проиллюстрировать формальное определение, мы посмотрим, как двумерное Якоби итерацию можно определить. Функция обновления вычисляет среднее арифметическое четырех соседей ячейки. В этом случае мы начинаем с начальным решением 0. Левая и правая границы зафиксированы на 1, а верхняя и нижняя границы установлены на 0. После достаточного числа итераций система сходится к седловидной форме.

{displaystyle {egin {align} I & = [0, ldots, 99] ^ {2} S & = mathbb {R} S_ {0} &: mathbb {Z} ^ {2} o mathbb {R} S_ { 0} ((x, y)) & = {egin {cases} 1, & x <0 0, & 0leq x <100 1, & xgeq 100end {cases}} s & = ((0, -1), (- 1,0), (1,0), (0,1)) T & двоеточие mathbb {R} ^ {4} o mathbb {R} T ((x_ {1}, x_ {2}, x_ {3} , x_ {4})) & = 0,25cdot (x_ {1} + x_ {2} + x_ {3} + x_ {4}) конец {выровнено}}}

{displaystyle S_ {0}}

{displaystyle S_ {200}}

{displaystyle S_ {400}}

{displaystyle S_ {600}}

{displaystyle S_ {800}}

{displaystyle S_ {1000}}

2D Итерация Якоби на

{displaystyle 100 ^ {2}}

Массив

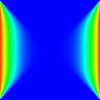
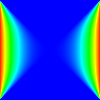
Трафареты

Форма окрестности, используемой во время обновлений, зависит от самого приложения. Чаще всего используются трафареты в 2D или 3D версиях район фон Неймана и Окрестности Мура. В приведенном выше примере используется двухмерный шаблон фон Неймана, в то время как коды LBM обычно используют его трехмерный вариант. Игра жизни Конвея использует 2D-окрестность Мура. Тем не менее, другие шаблоны, такие как шаблон из 25 точек для распространения сейсмических волн^[5] тоже можно найти.

9-точечный 2D-трафарет

5-точечный 2D-трафарет

7-точечный 3D-трафарет

25-точечный 3D-трафарет

Подборка трафаретов, используемых в различных научных приложениях.

Проблемы реализации

Многие коды моделирования могут быть естественно сформулированы как ISL. Поскольку время вычислений и потребление памяти линейно растут с количеством элементов массива, параллельные реализации ISL имеют первостепенное значение для исследований.^[6] Это сложно, поскольку вычисления тесно связаны (из-за того, что обновления ячеек зависят от соседних ячеек), и большинство ISL привязаны к памяти (то есть отношение обращений к памяти к вычислениям высокое).^[7] Практически все текущие параллельные архитектуры были исследованы для эффективного выполнения ISL;^[8] В данный момент GPGPU оказались наиболее эффективными.^[9]

Библиотеки

Из-за важности ISL для компьютерное моделирование и их высокие вычислительные требования, существует ряд усилий, направленных на создание повторно используемых библиотек для поддержки ученых в выполнении вычислений на основе шаблонов. Библиотеки в основном занимаются распараллеливанием, но могут также решать другие проблемы, такие как ввод-вывод, рулевое управление и контрольно-пропускной пункт. Их можно классифицировать по их API.

Библиотеки на основе патчей

Это традиционный дизайн. Библиотека управляет набором п-мерные скалярные массивы, к которым пользовательская программа может обращаться для выполнения обновлений. Библиотека обрабатывает синхронизацию границ (дублированная зона-призрак или ореол). Преимущество этого интерфейса в том, что пользовательская программа может перебирать массивы, что упрощает интеграцию унаследованного кода. ^[10]. Недостатком является то, что библиотека не может обрабатывать блокировку кеша (поскольку это должно выполняться в циклах^[11]) или обертывание API-вызовов для ускорителей (например, через CUDA или OpenCL). Реализации включают Кактус, среда для решения физических задач и WaLBerla.

Библиотеки на основе ячеек

Эти библиотеки перемещают интерфейс для обновления отдельных ячеек моделирования: отображаются только текущая ячейка и ее соседи, например через методы получения / установки. Преимущество этого подхода заключается в том, что библиотека может жестко контролировать, какие ячейки обновляются в каком порядке, что полезно не только для реализации блокировки кеша,^[9] но также для запуска того же кода на многоядерных процессорах и графических процессорах.^[12] Этот подход требует, чтобы пользователь перекомпилировал исходный код вместе с библиотекой. В противном случае потребуется вызов функции для каждого обновления ячейки, что серьезно снизит производительность. Это возможно только с такими методами, как шаблоны классов или метапрограммирование, что также является причиной того, что этот дизайн встречается только в более новых библиотеках. Примеры Physis и LibGeoDecomp.

Смотрите также

использованная литература

^ ^а ^б ^c Рот, Джеральд и др. (1997) Труды SC'97: Высокопроизводительные сети и вычисления. Компиляция трафаретов в высокопроизводительном Фортране.
^ ^а ^б ^c ^d Слоут, Питер М.А. и др. (28 мая 2002 г.) Вычислительная наука - ICCS 2002: Международная конференция, Амстердам, Нидерланды, 21–24 апреля 2002 г. Труды, часть I. Стр. 843. Издательство: Springer. ISBN 3-540-43591-3.
^ ^а ^б ^c Фей, Дитмар и др. (2010) Грид-вычисления: Eine Basistechnologie für Computational Science. Стр. 439. Издательство: Springer. ISBN 3-540-79746-7
^ Ян, Лоуренс Т .; Го, Миньи. (12 августа 2005 г.) Высокопроизводительные вычисления: парадигма и инфраструктура. Стр. 221. Издательство: Wiley-Interscience. ISBN 0-471-65471-X
^ Micikevicius, Paulius et al. (2009) Вычисление конечных разностей 3D на GPU с использованием CUDA Труды 2-го семинара по универсальной обработке на графических процессорах ISBN 978-1-60558-517-8
^ Датта, Кошик (2009) Автонастройка кодов трафаретов для многоядерных платформ на основе кэша В архиве 2012-10-08 в Wayback Machine, Кандидат наук. Тезис
^ Wellein, G et al. (2009) Эффективная временная блокировка для вычислений трафаретов за счет распараллеливания волнового фронта с учетом множества ядер, 33-я ежегодная Международная конференция по компьютерному программному обеспечению и приложениям IEEE, COMPSAC 2009
^ Датта, Каушик и др. (2008) Оптимизация трафаретных вычислений и автонастройка на современных многоядерных архитектурах, SC '08 Труды конференции ACM / IEEE 2008 года по суперкомпьютерам
^ ^а ^б Шефер, Андреас и Фей, Дитмар (2011) Высокопроизводительные алгоритмы кода трафарета для GPGPU, Труды Международной конференции по вычислительным наукам, ICCS 2011
^ С. Донат, Й. Гётц, К. Файхтингер, К. Иглбергер и У. Рюде (2010) waLBerla: Оптимизация для систем на базе Itanium с тысячами процессоров, Высокопроизводительные вычисления в науке и технике, Гархинг / Мюнхен, 2009 г.
^ Нгуен, Энтони и др. (2010) Оптимизация блоков 3.5-D для вычислений трафаретов на современных процессорах и графических процессорах, SC '10 Proceedings of the 2010 ACM / IEEE International Conference for High Performance Computing, Networking, Storage and Analysis
^ Наоя Маруяма, Тацуо Номура, Кенто Сато и Сатоши Мацуока (2011) Physis: модель неявно параллельного программирования для трафаретных вычислений на крупномасштабных суперкомпьютерах с GPU-ускорением, SC '11 Труды Международной конференции ACM / IEEE 2011 по высокопроизводительным вычислениям, сетям, хранению данных и анализу

внешние ссылки

[Roth-1] а ^б ^c Рот, Джеральд и др. (1997) Труды SC'97: Высокопроизводительные сети и вычисления. Компиляция трафаретов в высокопроизводительном Фортране.

[Sloot-2] а ^б ^c ^d Слоут, Питер М.А. и др. (28 мая 2002 г.) Вычислительная наука - ICCS 2002: Международная конференция, Амстердам, Нидерланды, 21–24 апреля 2002 г. Труды, часть I. Стр. 843. Издательство: Springer. ISBN 3-540-43591-3.

[Fey-3] а ^б ^c Фей, Дитмар и др. (2010) Грид-вычисления: Eine Basistechnologie für Computational Science. Стр. 439. Издательство: Springer. ISBN 3-540-79746-7

[4] Ян, Лоуренс Т .; Го, Миньи. (12 августа 2005 г.) Высокопроизводительные вычисления: парадигма и инфраструктура. Стр. 221. Издательство: Wiley-Interscience. ISBN 0-471-65471-X

[5] Micikevicius, Paulius et al. (2009) Вычисление конечных разностей 3D на GPU с использованием CUDA Труды 2-го семинара по универсальной обработке на графических процессорах ISBN 978-1-60558-517-8

[Datta-6] Датта, Кошик (2009) Автонастройка кодов трафаретов для многоядерных платформ на основе кэша В архиве 2012-10-08 в Wayback Machine, Кандидат наук. Тезис

[Wellein-7] Wellein, G et al. (2009) Эффективная временная блокировка для вычислений трафаретов за счет распараллеливания волнового фронта с учетом множества ядер, 33-я ежегодная Международная конференция по компьютерному программному обеспечению и приложениям IEEE, COMPSAC 2009

[datta2-8] Датта, Каушик и др. (2008) Оптимизация трафаретных вычислений и автонастройка на современных многоядерных архитектурах, SC '08 Труды конференции ACM / IEEE 2008 года по суперкомпьютерам

[schaefer-9] а ^б Шефер, Андреас и Фей, Дитмар (2011) Высокопроизводительные алгоритмы кода трафарета для GPGPU, Труды Международной конференции по вычислительным наукам, ICCS 2011

[walberla-10] С. Донат, Й. Гётц, К. Файхтингер, К. Иглбергер и У. Рюде (2010) waLBerla: Оптимизация для систем на базе Itanium с тысячами процессоров, Высокопроизводительные вычисления в науке и технике, Гархинг / Мюнхен, 2009 г.

[35dblocking-11] Нгуен, Энтони и др. (2010) Оптимизация блоков 3.5-D для вычислений трафаретов на современных процессорах и графических процессорах, SC '10 Proceedings of the 2010 ACM / IEEE International Conference for High Performance Computing, Networking, Storage and Analysis

[physis-12] Наоя Маруяма, Тацуо Номура, Кенто Сато и Сатоши Мацуока (2011) Physis: модель неявно параллельного программирования для трафаретных вычислений на крупномасштабных суперкомпьютерах с GPU-ускорением, SC '11 Труды Международной конференции ACM / IEEE 2011 по высокопроизводительным вычислениям, сетям, хранению данных и анализу

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]