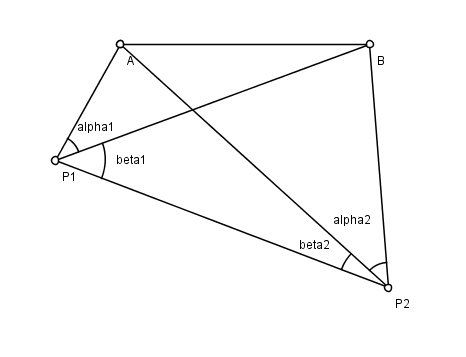
Проблема Хансенса - Hansens problem

Проблема Хансена проблема в плоском геодезия, названный в честь астронома Питер Андреас Хансен (1795–1874), работавший над геодезической съемкой Дании. Есть два известных момента А и B, и две неизвестные точки п₁ и п₂. Из п₁ и п₂ Наблюдатель измеряет углы линий обзора к каждой из трех других точек. Проблема в том, чтобы найти позиции п₁ и п₂. См. Рисунок; измеренные углы (α₁, β₁, α₂, β₂).

Поскольку она включает в себя наблюдения углов в неизвестных точках, проблема является примером резекция (в отличие от перекрестка).

Обзор метода решения

Определите следующие углы: γ = п₁AP₂, δ = п₁BP₂, φ = п₂AB, ψ = п₁BA. В качестве первого шага мы решим φ и ψСумма этих двух неизвестных углов равна сумме β₁ и β₂, что дает уравнение

{ displaystyle phi + psi = beta _ {1} + beta _ {2}.}

Второе уравнение можно найти более трудоемко, а именно: В закон синуса дает

{ displaystyle { frac {AB} {P_ {2} B}} = { frac { sin alpha _ {2}} { sin phi}}}

и

{ displaystyle { frac {P_ {2} B} {P_ {1} P_ {2}}} = { frac { sin beta _ {1}} { sin delta}}.}

Комбинируя их, мы получаем

{ displaystyle { frac {AB} {P_ {1} P_ {2}}} = { frac { sin alpha _ {2} sin beta _ {1}} { sin phi sin дельта}}.}

Совершенно аналогичные рассуждения с другой стороны дают

{ displaystyle { frac {AB} {P_ {1} P_ {2}}} = { frac { sin alpha _ {1} sin beta _ {2}} { sin psi sin гамма}}.}

Установка этих двух равных дает

{ displaystyle { frac { sin phi} { sin psi}} = { frac { sin gamma sin alpha _ {2} sin beta _ {1}} { sin delta sin alpha _ {1} sin beta _ {2}}} = k.}

Используя известный тригонометрическая идентичность это соотношение синусов можно выразить как тангенс угловой разности:

{ displaystyle tan { frac { phi - psi} {2}} = { frac {k-1} {k + 1}} tan { frac { phi + psi} {2}} .}

Это второе уравнение, которое нам нужно. Как только мы решим два уравнения для двух неизвестных ${ displaystyle phi}$ и ${ displaystyle psi}$ , мы можем использовать любое из двух приведенных выше выражений для ${ displaystyle { frac {AB} {P_ {1} P_ {2}}}}$ найти п₁п₂ поскольку AB известен. Затем мы можем найти все остальные сегменты, используя закон синусов.^[1]

Алгоритм решения

Нам даны четыре угла (α₁, β₁, α₂, β₂) и расстояние AB. Расчет происходит следующим образом:

Рассчитать ${ displaystyle gamma = pi - alpha _ {1} - beta _ {1} - beta _ {2}, quad delta = pi - alpha _ {2} - beta _ {1 } - beta _ {2}.}$
Рассчитать ${ Displaystyle к = { гидроразрыва { грех гамма грех альфа _ {2} грех бета _ {1}} { грех дельта грех альфа _ {1} грех бета _ {2 }}}.}$
Позволять ${ Displaystyle s = beta _ {1} + beta _ {2}, quad d = 2 arctan left [{ frac {k-1} {k + 1}} tan (s / 2) верно]}$ а потом ${ displaystyle phi = (s + d) / 2, quad psi = (s-d) / 2.}$
Рассчитать