Форм-фактор (электроника) - Form factor (electronics)

В электроника или электрические фактор формы из переменный ток форма волны (сигнал) - это отношение RMS (среднеквадратичное значение ) значение для Средняя стоимость (математическое среднее абсолютные значения всех точек на осциллограмме).^[1] Он определяет соотношение постоянный ток равной мощности относительно данного переменного тока. Первый также можно определить как постоянный ток, который будет производить эквивалентное тепло.^[2]

Расчет форм-фактора

Для идеальной непрерывной волновой функции по времени T среднеквадратичное значение может быть вычислено в интеграл форма:^[3]

${displaystyle X_{mathrm {rms} }={sqrt {{1 over {T}}{int _{t_{0}}^{t_{0}+T}{[x(t)]}^{2},dt}}}}$

В этом случае выпрямленное среднее значение является средним от интеграла абсолютного значения функции:^[3]

${displaystyle X_{mathrm {arv} }={1 over {T}}{int _{t_{0}}^{t_{0}+T}{|x(t)|,dt}}}$

В частное из этих двух значений - форм-фактор, ${displaystyle k_{mathrm {f} }}$, или в однозначных ситуациях, ${displaystyle k}$.

${displaystyle k_{mathrm {f} }={frac {mathrm {RMS} }{mathrm {ARV} }}={frac {sqrt {{1 over {T}}{int _{t_{0}}^{t_{0}+T}{[x(t)]}^{2},dt}}}{{1 over {T}}{int _{t_{0}}^{t_{0}+T}{|x(t)|,dt}}}}={frac {sqrt {Tint _{t_{0}}^{t_{0}+T}{{[x(t)]}^{2},dt}}}{int _{t_{0}}^{t_{0}+T}{|x(t)|,dt}}}}$

${displaystyle X_{mathrm {rms} }}$ отражает изменение расстояния функции от среднего и непропорционально сильно зависит от больших отклонений от неустановленного среднего значения.^[4]Он всегда будет не меньше, чем ${displaystyle X_{mathrm {arv} }}$, который измеряет только абсолютное расстояние от указанного среднего значения. Таким образом, форм-фактор не может быть меньше 1 (прямоугольная волна, где все мгновенные значения одинаково намного выше или ниже среднего значения; см. Ниже) и не имеет теоретического верхнего предела для функций с достаточным отклонением.

${displaystyle mathrm {RMS} _{mathrm {total} }={sqrt {{{mathrm {RMS} _{1}}^{2}}+{{mathrm {RMS} _{2}}^{2}}+...+{{mathrm {RMS} _{n}}^{2}}}}}$

может использоваться для объединения сигналов разных частот (например, для гармоник^[2]), а для той же частоты ${displaystyle mathrm {RMS} _{mathrm {total} }=mathrm {RMS} _{1}+mathrm {RMS} _{2}+...+mathrm {RMS} _{n}}$.

Поскольку АРВ в той же области можно суммировать как ${displaystyle mathrm {ARV} _{mathrm {total} }=mathrm {ARV} _{1}+mathrm {ARV} _{2}+...+mathrm {ARV} _{n}}$, форм-фактор сложной волны, состоящей из нескольких волн одной и той же частоты, иногда можно рассчитать как

${displaystyle k_{mathrm {f} _{mathrm {tot} }}={frac {mathrm {RMS} _{mathrm {tot} }}{mathrm {ARV} _{mathrm {tot} }}}={frac {mathrm {RMS} _{1}+...+mathrm {RMS} _{n}}{mathrm {ARV} _{1}+...+mathrm {ARV} _{n}}}}$.

Заявление

Цифровые измерительные приборы переменного тока часто создаются с учетом определенных форм сигналов. Например, многие цифровые мультиметры переменного тока специально масштабированы для отображения среднеквадратичного значения синусоидальной волны. Поскольку вычисление среднеквадратичного значения может быть затруднено в цифровом виде, вместо этого вычисляется абсолютное среднее значение, а результат умножается на форм-фактор синусоиды. Этот метод даст менее точные показания для сигналов, отличных от синусоидального сигнала.^[5]

Возведение в квадрат в RMS и абсолютное значение в ARV означает, что как значения, так и форм-фактор не зависят от знака волновой функции (и, следовательно, направления электрического сигнала) в любой точке. По этой причине форм-фактор такой же для волны, меняющей направление, с регулярным средним значением 0 и ее полностью выпрямленной версии.

Форм-фактор, ${displaystyle k_{mathrm {f} }}$, является наименьшим из трех волновых факторов, два других - пик фактор ${displaystyle k_{mathrm {a} }={frac {X_{mathrm {max} }}{X_{mathrm {rms} }}}}$ и менее известный коэффициент усреднения ${displaystyle k_{mathrm {av} }={frac {X_{mathrm {max} }}{X_{mathrm {arv} }}}}$.

${displaystyle k_{mathrm {av} }geq k_{mathrm {a} }geq k_{mathrm {f} }}$^[2]

Из-за их определений (все полагаются на Среднеквадратическое значение, Среднее выпрямленное значение и максимум амплитуда формы сигнала), эти три фактора связаны соотношением ${displaystyle k_{mathrm {av} }=k_{mathrm {a} }k_{mathrm {f} }}$,^[2] поэтому форм-фактор можно рассчитать с помощью ${displaystyle k_{mathrm {f} }={frac {k_{mathrm {av} }}{k_{mathrm {a} }}}}$.

Особые форм-факторы

${displaystyle a}$ представляет амплитуду функции и любые другие коэффициенты, применяемые в вертикальном измерении. Например, ${displaystyle 8sin(t)}$ можно проанализировать как ${displaystyle f(t)=asin(t), a=8}$. Поскольку и RMS, и ARV прямо пропорциональны ему, он не влияет на форм-фактор и может быть заменен нормализованной единицей для расчета этого значения.

${displaystyle D={frac { au }{T}}}$ это рабочий цикл, отношение времени «импульса» ${displaystyle au }$ (когда значение функции не равно нулю) до полной волны период ${displaystyle T}$. Большинство основных волновых функций достигают 0 только в бесконечно короткие моменты времени, и поэтому их можно рассматривать как имеющие ${displaystyle au =T,D=1}$. Однако к любой из перечисленных ниже неимпульсных функций можно добавить ${displaystyle {frac {sqrt {D}}{D}}={frac {1}{sqrt {D}}}={sqrt {frac {T}{ au }}}}$

чтобы позволить пульсацию. Это проиллюстрировано с помощью синусоидальной волны с полупрямым выпрямлением, которую можно рассматривать как импульсную полностью выпрямленную синусоидальную волну ${displaystyle D={frac {1}{2}}}$, и имеет ${displaystyle k_{mathrm {f} }=k_{mathrm {f} _{mathrm {frs} }}{sqrt {2}}}$.

Форма волны	Изображение	RMS	АРВ	Фактор формы
Синусоидальная волна		${displaystyle {frac {a}{sqrt {2}}}}$[2]	${displaystyle a{frac {2}{pi }}}$[2]	${displaystyle {frac {pi }{2{sqrt {2}}}}approx 1.11072073}$[3]
Полуволновой выпрямленный синус		${displaystyle {frac {a}{2}}}$	${displaystyle {frac {a}{pi }}}$	${displaystyle {frac {pi }{2}}approx 1.571}$
Двухполупериодный выпрямленный синус		${displaystyle {frac {a}{sqrt {2}}}}$	${displaystyle a{frac {2}{pi }}}$	${displaystyle {frac {pi }{2{sqrt {2}}}}}$
Квадратная волна, постоянное значение		${displaystyle a}$	${displaystyle a}$	${displaystyle {frac {a}{a}}=1}$
Пульсовая волна		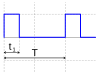${displaystyle a{sqrt {D}}}$[6]	${displaystyle aD}$	${displaystyle {frac {1}{sqrt {D}}}={sqrt {frac {T}{ au }}}}$
Треугольник волна		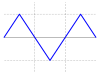${displaystyle {frac {a}{sqrt {3}}}}$[7]	${displaystyle {frac {a}{2}}}$	${displaystyle {frac {2}{sqrt {3}}}approx 1.15470054}$
Пилообразная волна		${displaystyle {frac {a}{sqrt {3}}}}$	${displaystyle {frac {a}{2}}}$	${displaystyle {frac {2}{sqrt {3}}}}$
Гауссовский белый шум U(-1,1)		${displaystyle {frac {1}{sqrt {3}}}}$[нужна цитата ]	${displaystyle {frac {1}{2}}}$[нужна цитата ]	${displaystyle {frac {2}{sqrt {3}}}}$

Рекомендации

1. Штутц, Майкл. «Измерение величины переменного тока». ОСНОВНАЯ ТЕОРИЯ AC. Получено 30 мая 2012.
2. Душа, Яцек; Гражина Гортат; Антони Лесьневский (2002). Подставы Мерниктва (Основы измерения) (по польски). Варшава: Wydawnictwo Politechniki Warszawskiej. С. 136–142, 197–203. ISBN  83-7207-344-9.
3. Енджеевский, Казимеж (2007). Laboratorium Podstaw Pomiarow (по польски). Варшава: Wydawnictwo Politechniki Warszawskiej. С. 86–87. ISBN  978-83-7207-4.
4. «Средняя абсолютная ошибка (MAE) и среднеквадратичная ошибка (RMSE)». Европейская виртуальная организация метеорологического обучения. Архивировано из оригинал 14 июля 2007 г.. Получено 30 мая 2012.
5. Танувиджая, Фрэнки. «Истинное среднеквадратичное значение по сравнению со средними выпрямленными показаниями мультиметра при переменном токе при использовании управления скоростью фазовой резки» (PDF). Esco Micro Pte Ltd. Получено 2012-12-13.
6. Настасье, Адриан. «Как получить среднеквадратичное значение импульсных и прямоугольных сигналов». Получено 9 июн 2012.
7. Настасье, Адриан. «Как получить среднеквадратичное значение треугольной формы волны». Получено 9 июн 2012.