Реактор непрерывного действия с мешалкой - Continuous stirred-tank reactor

Схема, показывающая установку реактора непрерывного действия с мешалкой.

В реактор непрерывного действия с мешалкой (CSTR), также известный как НДС- или же реактор обратного смешения, реактор со смешанным потоком (MFR) или непрерывный-поток реактор с мешалкой (CFSTR), является общей моделью для химический реактор в химическая инженерия и инженерия окружающей среды. CSTR часто относится к модели, используемой для оценки ключевых параметров работы блока при использовании реактора непрерывного действия с перемешиваемым резервуаром для достижения заданной производительности. Математическая модель работает для всех жидкостей: жидкостей, газов и суспензии.

Поведение CSTR часто аппроксимируется или моделируется поведением идеального CSTR, которое предполагает идеальное смешивание. В реакторе с идеальным перемешиванием реагент мгновенно и равномерно перемешивается по всему реактору при входе. Следовательно, состав на выходе идентичен составу материала внутри реактора, который является функцией времени пребывания и скорости реакции. CSTR является идеальным пределом полного перемешивания в конструкции реактора, что является полной противоположностью реактор идеального вытеснения (ПФР). На практике ни один из реакторов не ведет себя идеально, а вместо этого находится где-то между пределами смешивания идеального CSTR и PFR.

Идеальный CSTR

Схема поперечного сечения CSTR.

Моделирование

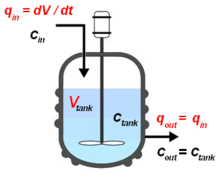
Непрерывный поток жидкости, содержащий неконсервативный химический реагент. А входит в идеальный CSTR объема V.

Предположения:

• идеальное или идеальное смешивание
• устойчивое состояние ${\displaystyle {\Bigl (}{\frac {dN_{A}}{dt}}=0{\Bigr )}}$, куда N_А количество родинок вида А
• закрытые границы
• постоянная жидкость плотность (действительно для большинства жидкостей; действительно для газов, только если нет чистого изменения количества молей или резкого изменения температуры)
• п^th-заказ реакция (р = kC_А^п), куда k - константа скорости реакции, C_А это концентрация видов А, и п это порядок реакции
• изотермический условия или постоянная температура (k постоянно)
• одиночный, необратимый реакция (ν_А = −1)
• Все реагенты А превращается в продукты в результате химической реакции
• N_А = C_А V

Интегральный баланс массы по количеству молей N_А видов А в реакторе объемом V:${\displaystyle 1.[{\text{Net accumulation of}}~A]=[A~{\text{in}}]-[A~{\text{out}}]+[{\text{Net generation of}}~A]}$

${\displaystyle 2.{\frac {dN_{A}}{dt}}=F_{Ao}-F_{A}+V\nu _{A}r_{A}}$^[1]

куда,

• F_АО молярная скорость потока частиц на входе А
• F_А молярная скорость потока на выходе А
• v_А это стехиометрический коэффициент
• р_А скорость реакции

Применяя допущения об установившемся состоянии и ν_А = −1, уравнение 2 упрощается до:

${\displaystyle 3.\ 0=F_{Ao}-F_{A}-Vr_{A}}$

Молярные скорости потока веществ А затем можно переписать в терминах концентрации А и расход жидкости (Q):

${\displaystyle 4.\ 0=QC_{Ao}-QC_{A}-Vr_{A}}$^[2]

Уравнение 4 затем можно переформулировать, чтобы выделить р_А и упрощено:

${\displaystyle 5.\ r_{A}={\frac {Q}{V}}(C_{Ao}-C_{A})}$^[2]

${\displaystyle 6.\ r_{A}={\frac {1}{\tau }}(C_{Ao}-C_{A})}$

куда,

• ${\displaystyle \tau }$ - теоретическое время пребывания (${\displaystyle \tau ={\tfrac {V}{Q}}}$)
• C_АО - входная концентрация частиц A
• C_А - концентрация вещества А на выходе из реактора / выхода

Время жительства - общее количество времени, которое дискретное количество реагента проводит внутри реактора. Для идеального реактора теоретическое время пребывания, ${\displaystyle \tau }$, всегда равна объему реактора, деленному на расход жидкости.^[2] См. Следующий раздел для более подробного обсуждения распределения времени пребывания CSTR.

В зависимости от порядок реакции, скорость реакции, р_А, как правило, зависит от концентрации видов А в реакторе и константа скорости. Ключевым допущением при моделировании CSTR является то, что любой реагент в жидкости идеально (то есть однородно) смешан в реакторе, подразумевая, что концентрация внутри реактора одинакова в выходящем потоке.^[3] Константа скорости может быть определена с использованием известной эмпирической скорости реакции, скорректированной с учетом температуры с помощью Температурная зависимость Аррениуса.^[2] Как правило, с повышением температуры увеличивается и скорость реакции.

Уравнение 6 может быть решено интегрированием после подстановки правильного выражения для скорости. В таблице ниже представлена ​​концентрация видов на выходе. А для идеального CSTR. Значения концентрации на выходе и времени пребывания являются основными критериями проектирования при разработке CSTR для промышленного применения.

Концентрация на выходе для идеального CSTR

Порядок реакции	CА
п = 0	${\displaystyle C_{A}={C_{Ao}}-{k\tau }}$
п = 1	${\displaystyle C_{A}={\frac {C_{Ao}}{1+k\tau }}}$[1]
п = 2	${\displaystyle C_{A}={\frac {-1+{\sqrt {1+4k\tau C_{Ao}}}}{2k\tau }}}$
Другое n	Требуется численное решение

Распределение времени проживания

Функции распределения по возрасту E (t) и кумулятивного распределения по возрасту F (t) для идеального CSTR.

Идеальный CSTR будет демонстрировать четко определенное поведение потока, которое может быть охарактеризовано реактором. распределение времени пребывания, или возрастное распределение выхода.^[4] Не все частицы жидкости будут проводить в реакторе одинаковое количество времени. Распределение возраста на выходе (E (t)) определяет вероятность того, что данная жидкая частица проведет время t в реакторе. Аналогичным образом, совокупное распределение возраста (F (t)) дает вероятность того, что данная жидкая частица имеет возраст выхода меньше времени t.^[3] Одним из ключевых выводов распределения возраста на выходе является то, что очень небольшое количество частиц жидкости никогда не покинет CSTR.^[5] В зависимости от применения реактора это может быть либо достоинством, либо недостатком.

Неидеальный CSTR

В то время как идеальная модель CSTR полезна для предсказания судьбы компонентов во время химического или биологического процесса, CSTR редко демонстрируют идеальное поведение в реальности.^[2] Чаще всего гидравлика реактора не работает идеально или условия в системе не соответствуют исходным предположениям. Идеальное смешивание - это теоретическая концепция, которая на практике недостижима.^[6] Однако для инженерных целей, если время пребывания в 5-10 раз превышает время перемешивания, предположение об идеальном перемешивании обычно остается верным.

Функции распределения возраста выхода E (t) и совокупного распределения возраста F (t) для CSTR с мертвым пространством.

Неидеальное гидравлическое поведение обычно классифицируется по мертвому пространству или короткому замыканию. Эти явления возникают, когда некоторая жидкость проводит в реакторе меньше времени, чем теоретическое время пребывания. ${\displaystyle \tau }$. Наличие углов или перегородок в реакторе часто приводит к образованию мертвого пространства, в котором жидкость плохо перемешивается.^[6] Точно так же струя жидкости в реакторе может вызвать короткое замыкание, при котором часть потока покидает реактор намного быстрее, чем основная масса жидкости. Если в CSTR возникает мертвое пространство или короткое замыкание, соответствующие химические или биологические реакции могут не завершиться до того, как жидкость покинет реактор.^[2] Любое отклонение от идеального потока приведет к распределению времени пребывания, отличному от идеального, как показано справа.

Моделирование неидеального потока

Хотя реакторы с идеальным потоком редко встречаются на практике, они являются полезными инструментами для моделирования реакторов с неидеальным потоком. Любой режим потока может быть достигнут путем моделирования реактора как комбинации идеальных CSTR и реакторы с поршневым потоком (PFR) либо последовательно, либо параллельно.^[6] Например, бесконечный ряд идеальных CSTR гидравлически эквивалентен идеальному PFR.^[2]

Для моделирования систем, которые не подчиняются предположениям о постоянной температуре и единственной реакции, необходимо учитывать дополнительные зависимые переменные. Если считается, что система находится в нестационарном состоянии, необходимо решить дифференциальное уравнение или систему связанных дифференциальных уравнений. Отклонения в поведении CSTR можно учесть с помощью дисперсионной модели. Известно, что CSTR являются одной из систем, которые демонстрируют сложное поведение, такое как установившаяся множественность, предельные циклы и хаос.

Приложения

CSTR облегчают быстрое разбавление реагентов путем перемешивания. Следовательно, для реакций ненулевого порядка низкая концентрация реагента в реакторе означает, что CSTR будет менее эффективным при удалении реагента по сравнению с PFR с тем же временем пребывания.^[3] Следовательно, CSTR обычно больше, чем PFR, что может быть проблемой в приложениях, где пространство ограничено. Однако одним из дополнительных преимуществ разбавления в CSTR является способность нейтрализовать потрясения системы. В отличие от PFR, характеристики CSTR менее подвержены изменениям во входящем составе, что делает их идеальными для различных промышленных применений:

Анаэробные варочные котлы на Станция очистки сточных вод Ньютаун-Крик в Гринпойнте, Бруклин.

Инженерия окружающей среды

• Процесс активированного ила для очистки сточных вод^[2]
• Системы очистки лагун для очистки естественных сточных вод^[2]
• Анаэробные варочные котлы для стабилизации твердых биологических веществ сточных вод^[7]

Химическая инженерия

• Петлевой реактор для фармацевтического производства^[8]

• Ферментация^[8]
• Производство биогаза

Смотрите также

• Ламинарный проточный реактор
• Микрореактор
• Колебательный реактор с перегородкой
• Модель реактора идеального вытеснения

Примечания

Рекомендации

1. Шмидт, Лэнни Д. (1998). Инженерия химических реакций. Нью-Йорк: Издательство Оксфордского университета. ISBN  0-19-510588-5.
2. Меткалф и Эдди (03.09.2013). Очистка сточных вод: очистка и восстановление ресурсов. Чобаноглоус, Джордж, Стенсель, Х. Дэвид, Цучихаши, Рюджиро, Бертон, Франклин Л. (Франклин Луис), 1927-, Абу-Орф, Мохаммад, Боуден, Грегори (Пятое изд.). Нью-Йорк, штат Нью-Йорк. ISBN  978-0-07-340118-8. OCLC  858915999.
3. Бенджамин, Марк М. (13.06.2013). Инженерия качества воды: процессы физической / химической очистки. Лоулер, Десмонд Ф. Хобокен, Нью-Джерси. ISBN  978-1-118-63227-7. OCLC  856567226.
4. Болин, Берт; Родх, Хеннинг (январь 1973 г.). «Заметка о понятиях возрастного распределения и времени прохождения в естественных водоемах». Скажи нам. 25 (1): 58–62. Дои:10.3402 / tellusa.v25i1.9644. ISSN  0040-2826.
5. Monsen, Nancy E .; Cloern, Джеймс Э .; Лукас, Лиза В .; Монисмит, Стивен Г. (сентябрь 2002 г.). «Комментарий об использовании времени промывки, времени пребывания и возраста в качестве шкалы времени транспортировки». Лимнология и океанография. 47 (5): 1545–1553. Bibcode:2002LimOc..47.1545M. Дои:10.4319 / lo.2002.47.5.1545.
6. Дэвис, Марк Э. (2003). Основы инженерии химических реакций. Дэвис, Роберт Дж. (Международный редактор). Бостон: Макгроу-Хилл. ISBN  978-1-62870-437-2. OCLC  880604539.
7. Hurtado, F.J .; Kaiser, A.S .; Замора, Б. (март 2015 г.). «Гидродинамический анализ реактора непрерывного действия с мешалкой для технической оптимизации сбраживания сточных вод». Водные исследования. 71: 282–293. Дои:10.1016 / j.watres.2014.11.053. ISSN  0043-1354. PMID  25635665.
8. «Визуальная энциклопедия химической инженерии». encyclopedia.che.engin.umich.edu. Получено 2020-04-30.