Топология схемы - Circuit topology
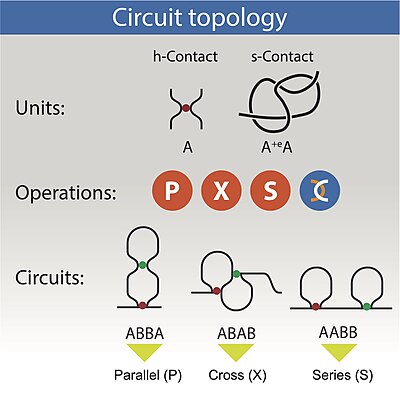
В топология схемы линейного полимер относится к расположению его внутримолекулярных контактов. Примеры линейных полимеров с внутримолекулярными контактами: нуклеиновые кислоты и белки. Для определения топологии схемы контакты определяются в зависимости от контекста. Для белков с дисульфидными связями эти связи можно рассматривать как контакты. В контексте, где взаимодействия бета-бета в белках более актуальны, эти взаимодействия используются для определения топологии цепи. Таким образом, структура топологии схем может применяться в широком диапазоне приложений, включая сворачивание белка и анализ геном архитектура.[1] В частности, данные из Ик и связанные технологии могут быть легко проанализированы с использованием структуры топологии схем.
Для цепи с двумя двоичными контактами доступны три варианта размещения: параллельный, последовательный и перекрестный. Для цепочки с n контактами топология может быть описана матрицей n на n, в которой каждый элемент иллюстрирует взаимосвязь между парой контактов и может принимать одно из трех состояний, P, S и X. Многовалентные контакты также могут быть категоризированы полностью или через разложение на несколько бинарных контактов. Точно так же топология схемы позволяет классифицировать попарное расположение пересечений цепей и клубков, тем самым обеспечивая полное трехмерное описание сложенных цепей.
Топология схемы имеет значение для кинетики сворачивания и молекулярной эволюции и была применена для создания полимеров, включая оригами белков. Топология схемы, а также порядок и размер контактов являются определяющими факторами скорости складывания линейных полимеров.[2] Топология клеточного протеома и естественной РНК отражает эволюционные ограничения биомолекулярных структур.[3] Топологический ландшафт биомолекул может быть охарактеризован, а эволюция молекул может быть изучена как переходные пути внутри ландшафта.[4]
дальнейшее чтение
- А. Головнев на эл., Обобщенная схемная топология свернутых линейных цепей. iScience (2020). связь
- Б. Скалвини и др., Топология свернутых молекулярных цепочек: от отдельных биомолекул до инженерного оригами. Тенденции в химии (2020) связь
- М. Хейдари и др., Анализ топологии цепи реакций сворачивания полимеров. ACS Central Science (2020) связь
Рекомендации
- ^ Машаги, Алиреза; van Wijk, Roeland J .; Танс, Сандер Дж. (2014). «Цепная топология белков и нуклеиновых кислот». Структура. 22 (9): 1227–1237. Дои:10.1016 / j.str.2014.06.015. PMID 25126961.
- ^ Мюглер, Эндрю; Загар, Сандер Дж .; Машаги, Алиреза (2014). «Схема топологии самовзаимодействующих цепей: последствия для сворачивания и разворачивания динамики». Phys. Chem. Chem. Phys. 16 (41): 22537–22544. Bibcode:2014PCCP ... 1622537M. Дои:10.1039 / C4CP03402C. PMID 25228051.
- ^ Машаги, Алиреза; Рамезанпур, Абольфазл (2015). «Схема топологии линейных полимеров: статистическая механическая обработка». RSC Adv. 5 (64): 51682–51689. arXiv:1509.00432. Дои:10.1039 / C5RA08106H. S2CID 62704705.
- ^ Машаги, Алиреза; Рамезанпур, Абольфазл (2015). «Меры расстояния и эволюция полимерных цепей в их топологическом пространстве». Мягкая материя. 11 (33): 6576–6585. arXiv:1509.00444. Bibcode:2015SMat ... 11.6576M. Дои:10.1039 / C5SM01482D. PMID 26189822. S2CID 36805814.
