Теорема Седербаумса о максимальном потоке - Cederbaums maximum flow theorem

Теорема Седербаума^[1] определяет гипотетические аналоговые электрические сети, которые автоматически дадут решение задача минимального размера s – t. В качестве альтернативы, симуляция такой сети также даст решение задачи минимального сокращения s – t. Эта статья дает основные определения, формулировку теоремы и доказательство теоремы. Изложение в этой статье близко следует изложения теоремы в оригинальной публикации.

Определения

Определения в этой статье во всех отношениях согласуются с определениями, данными при обсуждении теорема о максимальном потоке и минимальном сечении.

График потока

Теорема Седербаума применима к определенному типу ориентированного графа:  грамм = (V, E). V - это набор узлов. ${\displaystyle E}$ набор ориентированных ребер: ${\displaystyle E=(a,b)\in V\times V}$ С каждым ребром связан положительный вес:  ш_ab: E → р⁺. Два узла должны быть s и т: ${\displaystyle s\in V}$ и ${\displaystyle t\in V}$.

Поток

Поток,   ж : E → р⁺, - положительная величина, связанная с каждым ребром в графе. Поток ограничен весом связанного ребра и сохранением потока в каждой вершине, как описано здесь.

Текущий

Пара ребер.

Текущий определяется как карта для каждой пары ребер с действительные числа,  я_ab : E^п → р. Ток отображает напряжение в диапазоне, который определяется весами соответствующих переднего и обратного фронтов. Каждая пара ребер - это набор, состоящий из прямого и обратного ребер для данной пары вершин. Ток в прямом и обратном направлениях между парой узлов аддитивно инвертирует друг друга:  я_ab = −я_ба. Ток сохраняется в каждом внутреннем узле сети. Чистый ток на ${\displaystyle s}$ и ${\displaystyle t}$ узлов не равно нулю. Чистый ток на ${\displaystyle s}$ узел определяется как входной ток. Для набора соседей узла ${\displaystyle s}$, ${\displaystyle N_{s}}$:

${\displaystyle I_{in}=\sum _{b\in N_{s}}i_{sb}}$

Напряжение

Напряжение определяется как отображение набора пар ребер в действительные числа,  v_ab : E^п → р. Напряжение прямо аналогично электрическому напряжению в электрической сети. Напряжение в прямом и обратном направлениях между парой узлов является аддитивно инверсным друг другу:  v_ab = −v_ба. Входное напряжение - это сумма напряжений по набору фронтов, ${\displaystyle P_{ab}}$, образующих путь между ${\displaystyle s}$ и ${\displaystyle t}$ узлы.

${\displaystyle V_{in}=\sum _{(a,b)\in P_{ab}}v_{ab}}$

s–т резать

Минимальный s – t разрез для ориентированного графа. Все ребра имеют одинаковый вес.

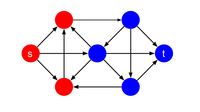
An s – t вырезать является разбиением графа на две части, каждая из которых содержит одну из ${\displaystyle s}$ или же ${\displaystyle t}$. Где ${\displaystyle S\cup T=V}$, ${\displaystyle \;\;s\in S}$, ${\displaystyle \;\;t\in T}$, s – t-разрез ${\displaystyle (S,T)}$. Набор s – t cut - это набор ребер, которые начинаются в ${\displaystyle S}$ и закончить ${\displaystyle T}$. Минимальный отрезок s – t - это отрезок s – t, набор отрезков которого имеет минимальный вес. Формально набор разрезов определяется как:

${\displaystyle X_{C}=\{(a,b)\in E\mid a\in S,b\in T\}}$

Электрическая сеть

Электрическая сеть - это модель, полученная из потокового графа. Каждый резистивный элемент в электрической сети соответствует паре ребер в потоковом графе. Положительный и отрицательный выводы электрической сети - это узлы, соответствующие ${\displaystyle s}$ и ${\displaystyle t}$ терминалы графа соответственно. Состояние напряжения модели становится двоичным в пределе, когда разница входного напряжения приближается к ${\displaystyle \infty }$. Поведение электрической сети определяется законами Кирхгофа по напряжению и току. Напряжения добавляются к нулю во всех замкнутых контурах, а токи складываются с нулем во всех узлах.

Резистивный элемент

Резистивный элемент в контексте этой теоремы - это компонент электрической сети, который соответствует паре ребер в потоковом графе.

iv характеристика

${\displaystyle iv}$ характеристика.

В ${\displaystyle iv}$ характеристика - это соотношение между током и напряжением. Требования:

(i) Ток и напряжение непрерывно зависят друг от друга.
(ii) Ток и напряжение являются неубывающими функциями друг относительно друга.
(iii) Диапазон тока ограничен весами переднего и обратного фронтов, соответствующих резистивному элементу. Текущий диапазон может включать или исключать конечные точки. Область напряжения не включает максимальный и минимальный токи:

 я_ab : р → [−ш_ab,ш_ба] или (-ш_ab,ш_ба] или [-ш_ab,ш_ба) или (-ш_ab,ш_ба)

 v_ab : (−ш_ab,ш_ба) → р

Формулировка теоремы

Предел тока  я_в между входными клеммами электрической сети в качестве входного напряжения, V_в подходы ${\displaystyle \infty }$, равняется весу минимального набора разрезов Икс_C.

${\displaystyle \lim _{V_{in}\rightarrow \infty }(I_{in})=\min _{X_{C}}\sum _{(a,b)\in X_{C}}w_{ab}.}$

Доказательство

Утверждение 1 Ток на любом резистивном элементе в электрической сети в любом направлении всегда меньше или равен максимальному потоку на соответствующем краю графика. Следовательно, максимальный ток через электрическую сеть меньше веса минимального среза потокового графа:

${\displaystyle \lim _{V_{in}\rightarrow \infty }(I_{in})\leq \min _{X_{C}}\sum _{(a,b)\in X_{C}}w_{ab}.}$

Утверждение 2 Как входное напряжение ${\displaystyle V_{in}}$ стремится к бесконечности, существует хотя бы один набор разрезов ${\displaystyle X'_{C}}$ таким образом, чтобы напряжение на отрезке приближалось к бесконечности.

${\displaystyle \exists X'_{C}\;\;\forall \;(a,b)\in X'_{C}\;\;\lim _{V_{in}\rightarrow \infty }(v_{ab})=\infty }$

Это означает, что:

${\displaystyle \lim _{V_{in}\rightarrow \infty }(I_{in})=\sum _{(a,b)\in X'_{C}}w_{ab}\;\geq \;\min _{X_{C}}\sum _{(a,b)\in X_{C}}w_{ab}.}$

Учитывая пункты 1 и 2 выше:

${\displaystyle \lim _{V_{in}\rightarrow \infty }(I_{in})=\min _{X_{C}}\sum _{(a,b)\in X_{C}}w_{ab}.}$

Похожие темы

Существование и единственность решения уравнений электрической сети, состоящей из монотонных резистивных элементов, было установлено Даффином.^[2]

Заявление

Теорема Седербаума о максимальном расходе является основой алгоритма Simcut.^{[3] [4]}

Рекомендации

1. Седербаум, И. (август 1962 г.). «Об оптимальной работе сетей связи». Журнал Института Франклина. 274: 130–141.
2. Даффин, Р. Дж. (1947). «Нелинейные сети. IIa». Бык. Амер. Математика. Soc. 10: 963--971.
3. Йим, П.Дж .: "Метод и система сегментации изображений, "Патент США US8929636, 6 января 2016 г.
4. Йим, П.Дж .: "Метод и система сегментации изображений с использованием ориентированного графа, "Патент США US9984311, 29 мая 2018 г.