Теорема Карно (перпендикуляры) - Carnots theorem (perpendiculars)
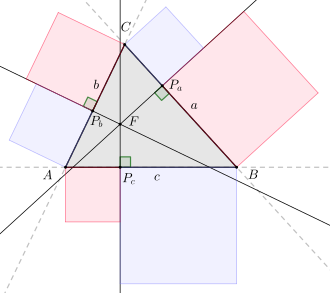
синяя область = красная область
Теорема Карно (названный в честь Лазар Карно ) описывает необходимое и достаточное условие для общей точки пересечения трех прямых, перпендикулярных (вытянутым) сторонам треугольника. Эту теорему также можно рассматривать как обобщение теорема Пифагора
Теорема
Для треугольника с боков рассмотрим три прямые, которые перпендикулярны сторонам треугольника и пересекаются в общей точке . Если точки педалей этих трех перпендикуляров по бокам , то имеет место следующее уравнение:
Обратное утверждение выше также верно, то есть, если уравнение верно для точек педалей трех перпендикуляров на трех сторонах треугольника, то они пересекаются в общей точке. Следовательно, уравнение обеспечивает необходимое и достаточное условие.
Особые случаи
Если треугольник имеет прямой угол в и точка пересечения расположен либо на или же , то приведенное выше уравнение дает теорему Пифагора. Например, если совпадает с тогда это дает , , , , и . Следовательно, приведенное выше уравнение преобразуется в теорему Пифагора .
Другое следствие - свойство серединных перпендикуляров треугольника пересекаться в общей точке. В случае серединного перпендикуляра у вас есть , и и, следовательно, справедливо указанное выше уравнение. что означает, что все три срединных перпендикуляра пересекаются в одной точке.
Рекомендации
- Вольгемут, Мартин, изд. (2010). Mathematisch für fortgeschrittene Anfänger: Weitere Bellebte Beiträge von Matroids Matheplanet (на немецком). Гейдельберг: Spektrum Akademischer Verlag. С. 273–276. ISBN 9783827426079. OCLC 699828882.
- Альфред С. Посаментьер; Чарльз Т. Салкинд (1996). Сложные задачи геометрии. Нью-Йорк: Дувр. С. 85–86. ISBN 9780486134864. OCLC 829151719.
внешняя ссылка
- Флориан Модлер: Vergessene Sätze am Dreieck - Der Satz von Carnot at matheplanet.com (немецкий)


















