Алгоритм без кеширования - Cache-oblivious algorithm

В вычисление, а алгоритм, не обращающий внимания на кеш (или алгоритм, превосходящий кэш) - это алгоритм разработан, чтобы воспользоваться Кэш процессора без размера кеша (или длины строки кеша и т. д.) в качестве явного параметра. An оптимальный алгоритм без кеширования алгоритм, не обращающий внимания на кеш, который оптимально использует кеш (в асимптотический смысл, игнорируя постоянные факторы). Таким образом, алгоритм без учета кэша предназначен для хорошей работы без изменений на нескольких машинах с разными размерами кеша или для иерархия памяти с разными уровнями кеша и разными размерами. Алгоритмы, не обращающие внимания на кэш, противопоставляются явным блокировка, как в оптимизация гнезда петель, который явно разбивает проблему на блоки, размер которых оптимален для данного кеша.

Оптимальные алгоритмы без учета кеша известны матричное умножение, транспонирование матрицы, сортировка, и ряд других проблем. Некоторые более общие алгоритмы, такие как БПФ Кули – Тьюки, оптимально не обращают внимания на кэш при определенном выборе параметров. Поскольку эти алгоритмы оптимальны только в асимптотическом смысле (без учета постоянных факторов), для получения почти оптимальной производительности в абсолютном смысле может потребоваться дополнительная настройка для конкретной машины. Цель алгоритмов, не обращающих внимания на кэш, - уменьшить объем такой настройки, которая требуется.

Как правило, алгоритм, не обращающий внимания на кэш, работает рекурсивный разделяй и властвуй алгоритм, где проблема делится на меньшие и меньшие подзадачи. В конце концов, каждый достигает размера подзадачи, который умещается в кеш, независимо от размера кеша. Например, оптимальное умножение матриц без учета кеширования получается путем рекурсивного деления каждой матрицы на четыре подматрицы для умножения, умножая подматрицы в в глубину мода. При настройке под конкретную машину можно использовать гибридный алгоритм который использует блокировку, настроенную для конкретных размеров кеша на нижнем уровне, но в остальном использует алгоритм без учета кеша.

История

Идея (и название) алгоритмов без учета кеша была придумана Чарльз Э. Лейзерсон еще в 1996 г. и впервые опубликованы Харальд Прокоп в своей магистерской диссертации на Массачусетский Институт Технологий в 1999 году.^[1] Было много предшественников, обычно анализирующих конкретные проблемы; они подробно обсуждаются в Frigo et al. 1999. Ранние процитированные примеры включают Singleton 1969 для рекурсивного быстрого преобразования Фурье, аналогичные идеи у Aggarwal et al. 1987, Frigo 1996 для умножения матриц и разложения LU, и Тодд Велдхёйзен 1996 для матричных алгоритмов в Блиц ++ библиотека.

Идеализированная модель кеша

Алгоритмы без учета кеша обычно анализируются с использованием идеализированной модели кеша, иногда называемой модель без кеширования. Эту модель намного проще анализировать, чем характеристики реального кеша (которые имеют сложную ассоциативность, политики замены и т. Д.), Но во многих случаях доказуемо в пределах постоянного коэффициента более реалистичной производительности кеша. Это отличается от модель внешней памяти потому что алгоритмы, не обращающие внимания на кеш, не знают размер блока или тайник размер.

В частности, модель без кеширования абстрактная машина (т.е. теоретический модель вычисления ). Это похоже на RAM модель машины который заменяет Машина Тьюринга Бесконечная лента с бесконечным массивом. К каждому месту в массиве можно получить доступ в ${\displaystyle O(1)}$ время, похожее на оперативная память на реальном компьютере. В отличие от модели RAM-машины, здесь также присутствует кэш: второй уровень хранения между RAM и CPU. Другие различия между двумя моделями перечислены ниже. В модели без кеширования:

Кэш слева содержит ${\displaystyle {\tfrac {M}{B}}}$ блоки размера ${\displaystyle B}$ каждый, в общей сложности M объекты. Объем внешней памяти справа неограничен.

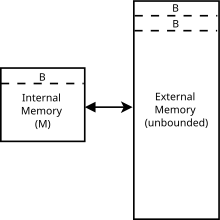
• Память разбита на блоки ${\displaystyle B}$ объекты каждый
• Груз или магазин между основная память и регистр ЦП теперь может обслуживаться из кэша.
• Если загрузка или хранилище не могут обслуживаться из кеша, это называется промах в кеше.
• Промах кэша приводит к загрузке одного блока из основной памяти в кеш. А именно, если ЦП пытается получить доступ к слову ${\displaystyle w}$ и ${\displaystyle x}$ это строка, содержащая ${\displaystyle w}$, тогда ${\displaystyle x}$ загружается в кеш. Если кэш был ранее заполнен, строка также будет исключена (см. Политику замены ниже).
• Кеш содержит ${\displaystyle M}$ объекты, где ${\displaystyle M=\Omega (B^{2})}$. Это также известно как предположение о высоком кэше.
• Кэш полностью ассоциативен: каждую строку можно загрузить в любое место кеша.^[2]
• Политика замены оптимальна. Другими словами, предполагается, что кеш-память получает всю последовательность обращений к памяти во время выполнения алгоритма. Если нужно вовремя выселить линию ${\displaystyle t}$, он проанализирует свою последовательность будущих запросов и исключит строку, к которой будет осуществляться самый дальний доступ в будущем. На практике это можно эмулировать с помощью Наименее недавно использованные политика, которая, как показано, находится в пределах небольшого постоянного коэффициента автономной оптимальной стратегии замены^[3][4]

Чтобы измерить сложность алгоритма, который выполняется в модели без учета кеширования, мы измеряем количество промахи в кеше что алгоритм переживает. Поскольку модель учитывает тот факт, что доступ к элементам в тайник намного быстрее, чем доступ к вещам в основная память, то Продолжительность алгоритма определяется только количеством передач памяти между кешем и основной памятью. Это похоже на модель внешней памяти, который имеет все вышеперечисленные функции, но алгоритмы без учета кеша не зависят от параметров кеша (${\displaystyle B}$ и ${\displaystyle M}$).^[5] Преимущество такого алгоритма состоит в том, что то, что эффективно на машине без кеширования, вероятно, будет эффективным на многих реальных машинах без точной настройки конкретных параметров реальной машины. Для многих проблем оптимальный алгоритм без учета кеша также будет оптимальным для машины с более чем двумя иерархия памяти уровни.^[3]

Примеры

Иллюстрация порядка строк и столбцов

Например, можно разработать вариант развернутые связанные списки который игнорирует кеш и позволяет обход списка N элементы в ${\displaystyle {\tfrac {N}{B}}}$ время, где B размер кеша в элементах.^{[нужна цитата ]} Для фиксированного B, это ${\displaystyle O(N)}$ время. Однако преимущество алгоритма заключается в том, что он может масштабироваться для использования преимуществ большего размера строки кэша (большие значения B).

Простейший алгоритм без учета кеширования, представленный Frigo et al. это неуместно матрица транспонировать операция (алгоритмы на месте также были разработаны для транспонирования, но намного сложнее для неквадратных матриц). Данный м×п множество А и п×м множество B, мы хотели бы сохранить транспонирование А в B. Наивное решение обходит один массив в порядке строк, а другой - в порядке столбцов. В результате, когда матрицы большие, мы получаем пропуск кеша на каждом этапе обхода по столбцам. Общее количество промахов кеша составляет ${\displaystyle \Theta (mn)}$.

Принцип алгоритма без кеширования для транспонирования матриц с использованием подхода «разделяй и властвуй». На графике показан рекурсивный шаг (а → б) разделения матрицы и транспонирования каждой части по отдельности.

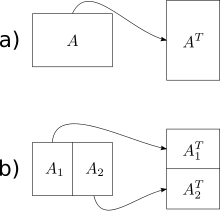
Алгоритм без кеширования имеет оптимальную сложность работы ${\displaystyle O(mn)}$ и оптимальная сложность кеша ${\displaystyle O(1+mn/B)}$. Основная идея состоит в том, чтобы свести транспонирование двух больших матриц к транспонированию малых (под) матриц. Мы делаем это, разделяя матрицы пополам по их большему измерению, пока нам не нужно просто выполнить транспонирование матрицы, которая поместится в кеш. Поскольку размер кеша неизвестен алгоритму, матрицы будут продолжать рекурсивно делиться даже после этого момента, но эти дальнейшие подразделения будут в кеше. Как только размеры м и п достаточно малы, поэтому Вход массив размера ${\displaystyle m\times n}$ и выходной массив размером ${\displaystyle n\times m}$ помещаются в кеш, обходы по строкам и столбцам приводят к ${\displaystyle O(mn)}$ работа и ${\displaystyle O(mn/B)}$ промахи в кэше. Используя этот подход «разделяй и властвуй», мы можем достичь того же уровня сложности для всей матрицы.

(В принципе, можно продолжать деление матриц до тех пор, пока не будет достигнут базовый вариант размера 1 × 1, но на практике используется более крупный базовый вариант (например, 16 × 16), чтобы амортизировать накладные расходы на вызовы рекурсивных подпрограмм.)

Большинство алгоритмов, не обращающих внимания на кэш, полагаются на подход «разделяй и властвуй». Они уменьшают проблему, так что в конечном итоге он помещается в кеш, независимо от того, насколько мал он, и заканчивают рекурсию на некотором небольшом размере, определяемом накладными расходами на вызов функции и аналогичными оптимизациями, не связанными с кешем, а затем используют некоторый эффективный доступ к кешу. шаблон для объединения результатов этих небольших решенных проблем.

Нравиться внешняя сортировка в модель внешней памяти, сортировка без учета кеширования возможна в двух вариантах: воронка сортировка, который напоминает Сортировка слиянием, и сортировка распределения без кеширования, который напоминает быстрая сортировка. Как и их аналоги с внешней памятью, оба имеют Продолжительность из ${\displaystyle O\left({\tfrac {N}{B}}\log _{\tfrac {M}{B}}{\tfrac {N}{B}}\right)}$, что соответствует нижняя граница и таким образом асимптотически оптимальный.^[5]

Смотрите также

• Алгоритм внешней памяти
• Funnelsort
• Сортировка распределения без учета кэша

Рекомендации

1. Харальд Прокоп. Алгоритмы, не обращающие внимания на кеш. Магистерская диссертация, Массачусетский технологический институт. 1999 г.
2. Кумар, Пиюш. «Алгоритмы, не обращающие внимания на кеш». Алгоритмы для иерархий памяти. LNCS 2625. Springer Verlag: 193–212. CiteSeerX  10.1.1.150.5426.
3. Frigo, M .; Лейзерсон, К.Э.; Прокоп, Х.; Рамачандран, С. (1999). Алгоритмы без кеширования (PDF). Proc. IEEE Symp. по основам компьютерных наук (FOCS). С. 285–297.
4. Дэниел Слейтор, Роберт Тарьян. Амортизированная эффективность правил обновления списков и разбивки на страницы. В Коммуникации ACM, Том 28, номер 2, стр.202-208. Февраль 1985 г.
5. Эрик Демейн. Не обращающие внимания на кеш алгоритмы и структуры данных, в конспектах лекций Летней школы EEF по массивным наборам данных, БРИКС, Орхусский университет, Дания, 27 июня - 1 июля 2002 г.