Диаграмма бабочки - Butterfly diagram

Эта статья посвящена диаграммам бабочек в алгоритмах БПФ. Диаграммы солнечных пятен см. Солнечный цикл.

График потока сигналов подключение входов Икс (слева) к выходам у которые зависят от них (справа) для шага «бабочка» БПФ Кули – Тьюки с основанием 2. Эта диаграмма напоминает бабочка (как в морфо бабочка показана для сравнения), отсюда и название, хотя в некоторых странах ее еще называют диаграммой песочных часов.

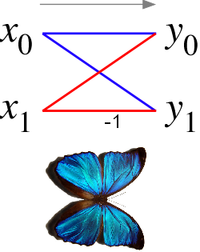
В контексте быстрое преобразование Фурье алгоритмы, а бабочка часть вычисления, которая объединяет результаты меньшего дискретные преобразования Фурье (ДПФ) в больший ДПФ или наоборот (разбиение большего ДПФ на частичные преобразования). Название «бабочка» происходит от формы диаграммы потока данных в случае radix-2, как описано ниже.^[1] Считается, что первое появление этого термина в печати относится к 1969 году. Массачусетский технологический институт технический отчет.^[2][3] Такую же структуру можно найти в Алгоритм Витерби, используется для поиска наиболее вероятной последовательности скрытых состояний.

Чаще всего термин «бабочка» встречается в контексте Алгоритм Кули – Тьюки БПФ, который рекурсивно разбивает ДПФ составной размер п = rm в р преобразование меньшего размера м куда р является "основанием" преобразования. Эти меньшие ДПФ затем объединяются через размер-р бабочки, которые сами являются ДПФ размером р (выполнила м раз на соответствующих выходах суб-преобразований), предварительно умноженные на корни единства (известный как факторы поворота ). (Это случай «прореживания по времени»; можно также выполнить шаги в обратном порядке, известные как «прореживание по частоте», когда бабочки идут первыми, а затем умножаются на множители тиддла. См. Также БПФ Кули – Тьюки статья.)

Диаграмма Radix-2 бабочка

В случае алгоритма Кули-Тьюки с основанием 2, бабочка - это просто ДПФ размера 2, которое принимает два входа (Икс₀, Икс₁) (соответствующие выходы двух суб-преобразований) и дает два выхода (у₀, у₁) по формуле (не включая факторы поворота ):

${\displaystyle y_{0}=x_{0}+x_{1}\,}$

${\displaystyle y_{1}=x_{0}-x_{1}.\,}$

Если нарисовать диаграмму потока данных для этой пары операций, (Икс₀, Икс₁) к (у₀, у₁) линии пересекаются и напоминают крылья бабочка, отсюда и название (см. также иллюстрацию справа).

БПФ с децимацией во времени по основанию 2 разбивает длинуN ДПФ на две длины-N/ 2 ДПФ, за которым следует этап комбинирования, состоящий из множества операций бабочки.

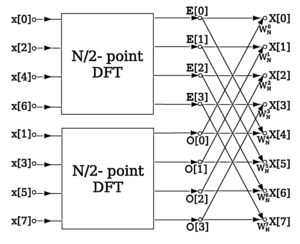
Более конкретно, алгоритм БПФ с децимацией во времени по основанию 2 на п = 2 ^п входы относительно примитива п-й корень из единства ${\displaystyle \omega _{n}^{k}=e^{-{\frac {2\pi ik}{n}}}}$ полагается на O (п бревно₂ п) бабочки вида:

${\displaystyle y_{0}=x_{0}+x_{1}\omega _{n}^{k}\,}$

${\displaystyle y_{1}=x_{0}-x_{1}\omega _{n}^{k},\,}$

куда k является целым числом, зависящим от вычисляемой части преобразования. Тогда как соответствующее обратное преобразование математически можно выполнить, заменив ω с ω⁻¹ (и, возможно, умножая на общий масштабный коэффициент, в зависимости от соглашения о нормализации), можно также напрямую инвертировать бабочек:

${\displaystyle x_{0}={\frac {1}{2}}(y_{0}+y_{1})\,}$

${\displaystyle x_{1}={\frac {\omega _{n}^{-k}}{2}}(y_{0}-y_{1}),\,}$

соответствующий алгоритму БПФ с децимацией по частоте.

Другое использование

Бабочка также может использоваться для улучшения случайности больших массивов частично случайных чисел, приводя каждое 32- или 64-битное слово в причинный контакт с каждым другим словом с помощью желаемого алгоритма хеширования, так что изменение любого одного бита имеет возможность изменения всех битов в большом массиве.^[4]

Смотрите также

• Математическая диаграмма
• Лемма Цассенхауза
• График потока сигналов

Рекомендации

1. Алан В. Оппенгейм, Рональд В. Шафер и Джон Р. Бак, Обработка сигналов в дискретном времени, 2-е издание (Верхняя Седл-Ривер, Нью-Джерси: Прентис-Холл, 1989)
2. К. Дж. Вайнштейн (1969-11-21). Эффекты квантования в цифровых фильтрах (Отчет). Лаборатория Линкольна Массачусетского технологического института. п. 42. Получено 2015-02-10. Это вычисление, называемое «бабочкой»
3. Сипра, Барри А. (2012-06-04). «Диаграмма БПФ и бабочки». mathoverflow.net. Получено 2015-02-10.
4. *Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, BP (2007), «Раздел 7.2 Полное хеширование большого массива», Числовые рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Издательство Кембриджского университета, ISBN  978-0-521-88068-8

внешняя ссылка

• объяснение диаграмм БПФ и бабочки.
• диаграммы бабочек различных реализаций БПФ (Radix-2, Radix-4, Split-Radix).