Обратное распространение во времени - Backpropagation through time
Эта статья может быть слишком техническим для большинства читателей, чтобы понять. |
Обратное распространение во времени (BPTT) - это градиент -основная методика тренировки определенных видов повторяющиеся нейронные сети. Его можно использовать для тренировки Сети Эльмана. Алгоритм был независимо разработан многочисленными исследователями.[1][2][3]
Алгоритм
Данные обучения для рекуррентной нейронной сети представляют собой упорядоченную последовательность пары ввода-вывода, . Для скрытого состояния необходимо указать начальное значение . Обычно для этой цели используется вектор всех нулей.
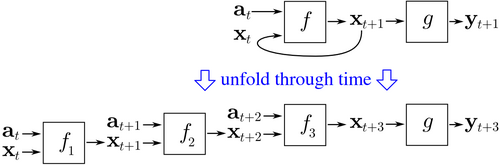
BPTT начинается с развертывания повторяющейся нейронной сети во времени. Развернутая сеть содержит входы и выходы, но все копии сети имеют одни и те же параметры. Тогда обратное распространение алгоритм используется для определения градиента стоимости по всем параметрам сети.
Рассмотрим пример нейронной сети, содержащей повторяющийся слой и прямая связь слой . Есть разные способы определения стоимости обучения, но общая стоимость всегда является средней стоимостью каждого временного шага. Стоимость каждого временного шага можно рассчитать отдельно. На рисунке выше показано, как стоимость во времени можно вычислить, развернув повторяющийся слой для трех временных шагов и добавление слоя прямой связи . Каждый экземпляр в развернутой сети имеет те же параметры. Таким образом, вес обновляется в каждом случае () суммируются.
Псевдокод
Псевдокод для усеченной версии BPTT, где обучающие данные содержат пары ввода-вывода, но сеть развернута на временные шаги:
Back_Propagation_Through_Time (a, y) // a [t] - это вход во время t. y [t] - выход Разверните сеть, чтобы она содержала k экземпляры ж делать до тех пор, пока не будут выполнены критерии остановки: x: = вектор нулевой величины // x - текущий контекст за т из 0 к п - к делать // t - время. n - длина обучающей последовательности. Установите входные данные сети равными x, a [t], a [t + 1], ..., a [t + k − 1] p: = распространить входные данные вперед по всей развернутая сеть e: = y [t + k] - p; // error = target - prediction Обратное распространение ошибки, e, обратно по всей развернутой сети Суммирует изменения веса в k экземплярах f вместе. Обновите все веса в f и g. x: = f (x, a [t]); // вычисляем контекст для следующего временного шага
Преимущества
BPTT имеет тенденцию быть значительно быстрее для обучения рекуррентных нейронных сетей, чем универсальные методы оптимизации, такие как эволюционный оптимизация.[4]
Недостатки
BPTT испытывает трудности с локальным оптимумом. Для рекуррентных нейронных сетей локальные оптимумы представляют собой гораздо более серьезную проблему, чем для нейронных сетей с прямой связью.[5] Периодическая обратная связь в таких сетях имеет тенденцию создавать хаотические отклики на поверхности ошибки, что приводит к частому возникновению локальных оптимумов и в плохих местах на поверхности ошибки.
Смотрите также
Рекомендации
- ^ Мозер, М. К. (1995). «Сфокусированный алгоритм обратного распространения ошибки для распознавания временных образов». В Chauvin, Y .; Румелхарт, Д. (ред.). Обратное распространение: теория, архитектуры и приложения. ResearchGate. Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс. стр. 137–169. Получено 2017-08-21.
- ^ Робинсон, А. Дж. И Фолсайд, Ф. (1987). Сеть динамического распространения ошибок, управляемая коммунальными предприятиями (Технический отчет). Кембриджский университет, инженерный факультет. CUED / F-INFENG / TR.1.
- ^ Вербос, Пол Дж. (1988). «Обобщение обратного распространения ошибки применительно к повторяющейся модели газового рынка». Нейронные сети. 1 (4): 339–356. Дои:10.1016 / 0893-6080 (88) 90007-х.
- ^ Сьёберг, Йонас; Чжан, Цинхуа; Люнг, Леннарт; Бенвенист, Альберт; Делион, Бернар; Глореннек, Пьер-Ив; Хьялмарссон, Хокан; Юдицкий, Анатолий (1995). «Нелинейное моделирование методом черного ящика в идентификации систем: единый обзор». Automatica. 31 (12): 1691–1724. CiteSeerX 10.1.1.27.81. Дои:10.1016/0005-1098(95)00120-8.
- ^ М.П. Куэльяр, М. Дельгадо и М.К. Пегалахар (2006). «Применение нелинейного программирования для обучения рекуррентных нейронных сетей в задачах прогнозирования временных рядов». Информационные системы предприятия VII. Springer Нидерланды. С. 95–102. Дои:10.1007/978-1-4020-5347-4_11. ISBN 978-1-4020-5323-8. Отсутствует или пусто
| название =(помощь)








